Analisi di raggiungibilità temporale

Rassegnatici dunque alla necessità di creare nuove tecniche di analisi specifiche per le reti temporizzate iniziamo a parlare di analisi dinamica a partire dall’analisi di raggiungibilità, ovvero la tecnica con cui nelle reti di Petri classiche eravamo in grado di enumerare gli stati finiti raggiungibili.

Provando ad adottare lo stesso approccio nei confronti delle reti TB ci si rende però subito conto di un enorme problema: le reti temporizzate hanno sempre infiniti stati, in quanto lo scatto di una singola transizione può produrre un’infinità di stati di arrivo che si differenziano unicamente per il timestamp dei gettoni generati. Sebbene la marcatura sia identica, le informazioni temporali legate ai gettoni sono differenti, distinguendo così ciascuno di tali stati della rete.
Bisogna inoltre considerare che per sua stessa natura il tempo avanza, rendendo così le reti temporizzate in grado di evolvere all’infinito: anche raggiungendo una marcatura che non abilita alcuna transizione, la rete continua ad evolvere in quanto il tempo corrente continua ad avanzare.

Dovendo costruire un albero di raggiungibilità questo sarebbe quindi sicuramente infinito, anche se in un modo diverso rispetto a quanto già visto per le reti non limitate: in quel caso infatti i gettoni non erano distinguibili, cosa che ci aveva permesso di raggrupparne un numero qualsiasi sotto il simbolo $\omega$, mentre in questo caso le differenze nei timestamp impediscono un simile approccio.

Al contrario, per ottenere per le reti TB un’analisi simile all’analisi di raggiungibilità delle reti classiche è necessario ridefinire completamente il concetto di stato raggiungibile.

Stati simbolici

Per riformulare il concetto stesso di raggiungibilità partiamo da innanzitutto da quello di marcatura: nelle reti temporizzate queste associavano infatti a ciascun posto un multiset in cui ad ogni timestamp era associato il numero di gettoni con tale timestamp presente nel posto.

Per evitare la difficoltà di distinguere tra gettoni con timestamp diversi viene introdotto nelle reti TB il concetto di stato simbolico, un oggetto matematico che sostituendo ai timestamp specifici degli identificatori simbolici dei gettoni permette di rappresentare un insieme di possibili stati con in comune lo stesso numero di gettoni in ciascun posto (esattamente come la marcatura delle reti classiche).

Più formalmente, uno stato simbolico è una tupla $[\mu, C]$, dove:

$\mu$ è la marcatura simbolica, che associa a ciascun posto un multiset di identificatori simbolici che rappresentano i timestamp dei gettoni in tale posto. Timestamp uguali saranno rappresentati dallo stesso simbolo, anche se si trovano in posti diversi: questo permette di mantenere l’identità tra timestamp;
$C$ è un sistema di vincoli (constraint), ovvero equazioni e disequazioni che rappresentano le relazioni tra gli identificatori simbolici dei gettoni. In questo modo è possibile mantenere le relazioni tra i timestamp dei gettoni pur non rappresentando esplicitamente il loro valore.

Un’esempio aiuterà a chiarire ogni dubbio. Immaginiamo di avere una rete TB con 3 posti $(P1, P2, P3)$, ciascuno con un solo gettone al loro interno, e la seguente marcatura iniziale: $\langle {0}, {1}, {0} \rangle$. Volendoci disfare dei timestamp espliciti dei gettoni, che tutto sommato ci interessano relativamente, dobbiamo mantenere due informazioni:

che i gettoni in $P1$ e $P3$ hanno lo stesso timestamp;
che il gettone in $P2$ ha timestamp maggiore di 1 del timestamp dei gettoni negli altri due posti.

Per fare ciò lo stato simbolico generato assegnerà lo stesso identificatore ai gettoni in $P1$ e $P3$ e espliciterà nei vincoli la relazione tra tempi. Otterremo dunque lo stato simbolico iniziale:

$$ \mu(P1)={\tau_0}, \: \: \: \mu(P2)={\tau_1}, \: \: \: \mu(P3)={\tau_0} $$

$$ C_0: \: \: \: \tau_1=\tau_0+1 $$

Infine, ci si potrebbe accorgere che in realtà non ci interessa che il timestamp del gettone in $P2$ sia esattamente $\tau_0+1$, ma solamente che esso sia maggiore di $\tau_0$. Ecco dunque che spesso si mutano i vincoli in disequazioni:

$$ C_0: \: \: \: \tau_0<\tau_1 $$

Albero di raggiungibilità temporale

Utilizzando la definizione di stato simbolico appena vista è possibile costruire tramite un algoritmo un albero di raggiungibilità temporale, in cui gli stati distinguibili solo dai timestamp vengono condensati in stati simbolici che conservano però le molteplicità dei gettoni nei posti e le relazioni tra i timestamp.

Prima di fare ciò, però, è necessario rinnovare un’assunzione già fatta in precedenza: anche in questa analisi assumeremo che le funzioni temporali $tf_{t}$ associate alle transizioni siano esprimibili come intervalli con estremi inclusi $\bf{[tmin_t, tmax_t]}$, dove questi ultimi possono dipendere ovviamente dai timestamp dei token in ingresso nonché da tempi assoluti.

Fatte queste premesse, possiamo partire a costruire effettivamente l’albero di raggiungibilità temporale di una rete TB secondo il seguente algoritmo:

Inizializzazione: si trasforma la marcatura iniziale della rete in uno stato simbolico, introducendo una serie di vincoli che descrivano le (pre-)condizioni iniziali della rete. Tale stato viene poi trasformato in un nodo, diventando la radice dell’albero, e aggiunto alla lista dei nodi da esaminare;
Scelta del prossimo nodo: tra i nodi dell’albero non ancora esaminati si seleziona il prossimo nodo da ispezionare;
Identificazione delle abilitazioni: in base allo stato simbolico rappresentato dal nodo si individuano le transizioni abilitate al suo interno;
Aggiornamento di marcatura e vincoli: ciascuna transizione abilitata trovata viene fatta scattare generando un nuovo stato simbolico, che viene rappresentato nell’albero come nodo figlio del nodo considerato e aggiunto alla lista dei nodi da esaminare;
Iterazione: si ritorna al punto 2.

Di questo semplice algoritmo approfondiamo dunque le due fasi più interessanti: l’aggiornamento di marcatura e vincoli e l’identificazione delle abilitazioni.

Aggiornamento di marcatura e vincoli

Come si fa a generare un nuovo stato simbolico a partire dallo stato simbolico corrente quando scatta una transizione abilitata? Sostanzialmente il processo si divide in due fasi: la creazione e distruzione di gettoni e l’espansione dei vincoli.

Il primo step è abbastanza semplice: è sufficiente distruggere i gettoni e i relativi simboli nel preset della transizione e generare nuovi gettoni nel suo postset, questi ultimi identificati tutti dallo stesso nuovo identificatore simbolico.

La generazione di nuovi vincoli è invece più complessa. Essa deve infatti tenere in considerazione quattro diversi aspetti:

I vecchi vincoli devono continuare a valere: essi esprimono infatti relazioni tra gli identificatori temporali che non possono essere alterate dallo scatto di una transizione;
Il nuovo timestamp deve avere il valore massimo nella rete: esso rappresenta infatti il tempo di scatto dell’ultima transizione scattata, e per monotonicità del tempo esso dovrà essere maggiore di tutti gli altri;
Il nuovo timestamp dev’essere compreso nell’intervallo dei possibili tempi di scatto della transizione scattata;
Il nuovo timestamp dev’essere minore del massimo tempo di scatto di tutte le transizioni forti abilitate il cui intervallo di scatto non sia nullo: per la semantica temporale forte, infatti, se così non fosse la transizione non potrebbe scattare prima che tale transizione forte scatti (cambiando anche potenzialmente l’insieme delle transizioni abilitate).

Tutte queste considerazioni devono essere condensate in un’unica espressione logica. Si dimostra quindi che dato uno stato simbolico precedente avente vincoli $C_n$, detto $maxT$ il timestamp massimo all’interno della rete e $\tau{n+1}$ l’identificatore simbolico dei gettoni generati dalla transizione $t$ è possibile definire i vincoli dello stato simbolico prodotto con la seguente formula_:

$$ \boxed{ \begin{align*} C_{n+1} = \: & C_n \wedge \tau_{n+1} \geq maxT \: \wedge tmin_t \leq \tau_{n+1} \leq tmax_t \\ & \bigcap\limits_{t_{STS}}(tmax_{t_{STS}} < tmin_{t_{STS}} \vee tmax_{t_{STS}} < maxT \vee tmax_{t_{STS}} \geq \tau_{n+1} ) \end{align*} } $$

dove per $t_{STS}$ si intende una qualunque transizione forte diversa da $t$; per ciascuna di esse bisognerà infatti aggiungere la condizione tra parentesi, relativa appunto alla semantica STS.

Tale catena di condizioni può ben presto diventare soverchiante, ma fortunatamente essa può essere semplificata sfruttando le implicazioni e le proprietà degli operatori logici. In particolare:

se una condizione $A$ implica un’altra condizione $B$ con cui è in AND ($\wedge$), allora la condizione implicata $B$ può essere cancellata;
se una condizione $A$ implica un’altra condizione $B$ con cui è in OR ($\vee$), allora la condizione implicante $A$ può essere cancellata.

Identificazione delle abilitazioni

Al contrario di quanto ci si potrebbe aspettare, però, la creazione di questo nuova catena di vincoli non è relegata alla sola creazione di un nuovo stato simbolico, ma è invece necessaria anche per identificare le transizioni abilitate. Avendo infatti introdotto degli identificatori simbolici che mascherano i timestamp dei gettoni, capire se una transizione sia abilitata o meno non è più così facile.

Tuttavia, è possibile dimostrare che la soddisfacibilità del vincolo generato da un eventuale scatto della transizione implica la sua abilitazione: se esiste cioè un assegnamento di timestamp agli identificatori simbolici che rende vero il vincolo allora la transizione è abilitata e può scattare. Il motivo di ciò appare evidente quando ci si accorge che nella generazione del vincolo abbiamo già tenuto in conto di tutti gli aspetti che avremmo osservato per stabilire se la transizione fosse abilitata o meno.

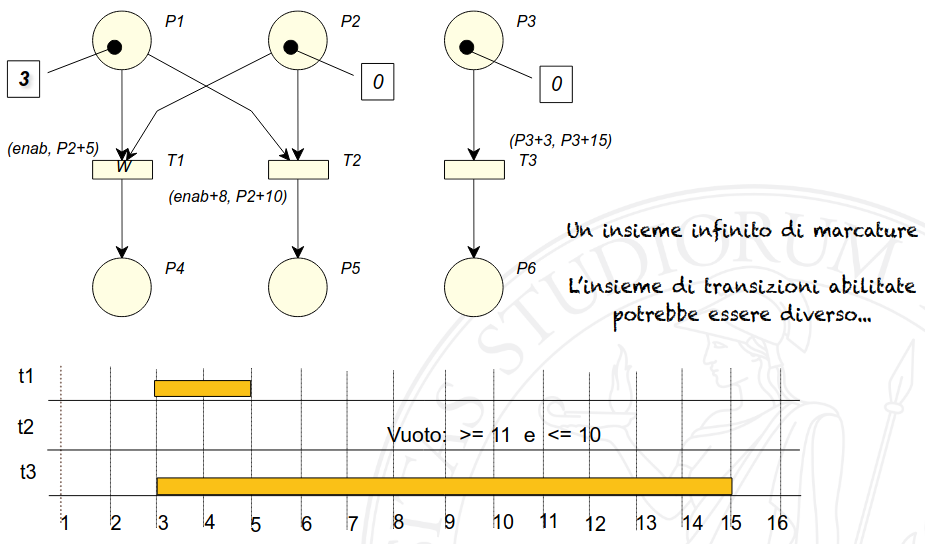
Proprio riguardo la soddisfacibilità viene poi fatta una distinzione a livello grafico nell’albero: essendo gli stati simbolici insiemi di marcature è possibile che una transizione sia abilitata in alcune di esse mentre è disabilitata in altre.
Quando questo succede, lo stato generato dalla transizione potrebbe essere uno stato finale, in quanto potrebbe aver disabilitato tutte le transizioni: ciò si comunica graficamente con un nodo circolare, mentre i nodi (e quindi gli stati) i cui vincoli sono sempre soddisfacibili si indicano con dei nodo rettangolari.

Alcuni operano poi una distinzione sulle frecce che collegano i nodi dell’albero: una freccia con punta nera indica che la transizione è sempre possibile, mentre una freccia con alla base un pallino bianco indica che per rendere possibile la transizione è stato violato qualche parte del vincolo, per cui non è detto che la transizione sia possibile in nessuna delle marcature rappresentate dallo stato simbolico.

Proprietà bounded

Eseguendo l’algoritmo a mano per un paio di iterazioni ci si rende ben presto conto di una cosa: il processo non termina!

Questo è dovuto al fatto che non avendo una forma normale per i vincoli che permetta di confrontare tra di loro gli stati simbolici non è possibile stabilire se si sia già visitato o meno uno stato: i vincoli si allungano così sempre di più, creando sempre stati simbolici nuovi (almeno sulla carta).

Si ottiene cioè un albero infinito. Nonostante ciò, tale albero è comunque particolarmente utile perché permette di verificare proprietà entro un certo limite di tempo: si parla per esempio di bounded liveness e bounded invariance, delle caratteristiche molto preziose sopratutto per lo studio dei sistemi Hard Real-Time.

Dall’albero al grafo aciclico

Esattamente come per le reti di Petri classiche, costruito l’albero di raggiungibilità ci piacerebbe ristrutturarlo per trasformarlo in un grafo che illustri più concisamente l’evoluzione del sistema rappresentato dalla rete. Di certo non possiamo sperare di ottenere un grafo ciclico in quanto per sua stessa natura il tempo non può tornare indietro, ma c’è qualche chance di ottenere un grafo aciclico?

Abbiamo già detto che a causa di come sono costruiti i nuovi stati simbolici è impossibile riottenere più volte lo stesso esatto stato. Ammettendo tuttavia di dimenticare la storia di come si è giunti in un certo nodo (ovvero l’insieme di transizioni che hanno portato ad esso) si potrebbe sperare di ritrovare alcuni stati che pur caratterizzati da storie diverse possiedono la stessa marcatura simbolica e lo stesso insieme di vincoli sugli identificatori simbolici presenti al suo interno.

Vediamo dunque una serie di tecniche che permettono, al costo di perdere una serie di informazioni, di individuare le somiglianze tra diversi stati simbolici in modo da raggrupparli in una serie di “super-stati” che fungano da nodi per il grafo che intendiamo costruire.

Semplificare i vincoli: l’algoritmo di Floyd

Per dimenticare la storia di come si è giunti in un certo stato simbolico è innanzitutto necessario semplificare i vincoli: come abbiamo visto nella formula precedente, ogni nuovo stato simbolico ereditava infatti i vincoli del precedente, cosa che permette di distinguere marcature identiche a cui si è giunti in modo diverso.

È dunque necessario esprimere i vincoli solo in termini della marcatura corrente: possiamo infatti considerare i vincoli sugli identificatori simbolici non più presenti nella rete come sostanzialmente inutili. Tuttavia, non basta cancellarli per risolvere la questione: sebbene il simbolo a cui fanno riferimento sia scomparso, essi potrebbero ancora esprimere vincoli indiretti sugli identificatori ancora presenti nella marcatura, che vanno ovviamente mantenuti. \ Si immagini per esempio di avere i vincoli $B - A \leq 5$ e $C - B \leq 6$ e che l’identificatore $B$ sia ormai scomparso dalla rete. Sebbene si riferiscano a un simbolo ormai non più presente, tali vincoli contengono ancora delle informazioni: sommando le due disequazioni membro a membro si ottiene infatti che $C - A \leq 11$, un vincolo su variabili presenti che era espresso indirettamente.

Per rimappare in modo semplice gli effetti dei vincoli sulle variabili non più presenti nella marcatura su quelle presenti si utilizza spesso l’algoritmo di Floyd, che funziona come segue:

Si riconducono tutti i vincoli alla forma $\bf{A - B \leq k}$, dove $A$ e $B$ sono identificatori simbolici e $k$ è una costante numerica; per esempio:

$$ A+2 \leq B \leq A+5 \: \: \: \longrightarrow \: \: \: A - B \leq -2 \: \text{ e } \: B - A \leq 5 $$

$$ B \leq C \leq B+6 \: \: \: \longrightarrow \: \: \: B - C \leq 0 \: \text{ e } \: C- B \leq 6 $$
Si costruisce una matrice in cui ad ogni riga e colonna corrisponde un identificatore simbolico e l’intersezione tra la riga $A$ e la colonna $B$ corrisponde al valore $\bf{k}$ tale per cui $\bf{A - B \leq k}$ in base ai vincoli ricavati al punto precedente, mentre per i valori non noti si scrive semplicemente un punto di domanda;
Si riempiono tutti i posti contrassegnati da punti di domanda utilizzando la seguente formula:

$$ \boxed{m[i,j] = m[i,k] + m[k,j]} $$

che mima la somma membro a membro delle disequazioni che rappresentano i vincoli. In questo modo è possibile scoprire i vincoli indiretti tra variabili;
Si esplicitano i vincoli indiretti relativi agli identificatori simbolici presenti nella marcatura corrente e si eliminano i vincoli che contengono gli identificatori non inclusi.

Applicato l’algoritmo di Floyd, ottenuti i vincoli impliciti ed eliminati i vincoli contenenti identificatori simbolici è possibile semplificare di molto l’insieme dei vincoli di nodi del grafo, identificando anche le prime somiglianze tra nodi.

Inclusione tra stati

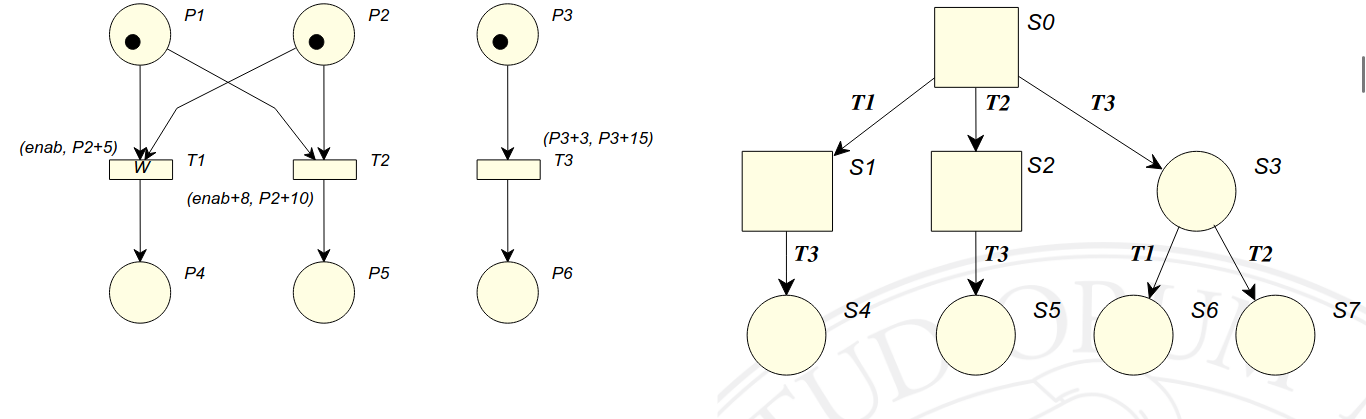
Il raggruppamento offerto dalla semplificazione dei vincoli tramite l’algoritmo di Floyd non è però sufficiente a ottenere grafi aciclici soddisfacenti. Si consideri per esempio la rete in figura:

Come si vede, essa genera una serie di nodi nel grafo di raggiungibilità tutti diversi nonostante essi abbiano la stessa marcatura e l’unica differenza sia data dalla costante nel vincolo. Per semplificare situazioni come queste viene introdotto il concetto di inclusione (o contenimento) tra stati: sapendo infatti che gli stati simbolici rappresentano insiemi di marcature è opportuno chiedersi se alcuni di essi possano essere sottoinsiemi di altri.

Ecco dunque che si dice che uno stato $A$ è contenuto in un altro stato $B$ se e solo se tutte le marcature rappresentate da $A$ sono rappresentate anche da $B$. Ciò avviene quando:

$A$ e $B$ hanno lo stesso assegnamento di timestamp;
i vincoli di $A$ implicano i vincoli di $B$, ovvero $C_A \rightarrow C_B$.

Decidiamo quindi di rappresentare nel grafo solo gli stati contenuti, introducendo però una distinzione grafica: la punta bianca della freccia indica che spostandosi lungo di essa si arriva ad un sottoinsieme del “super-stato” di arrivo, ovvero uno stato avente vincoli più stringenti di quelli mostrati.

Tempi relativi

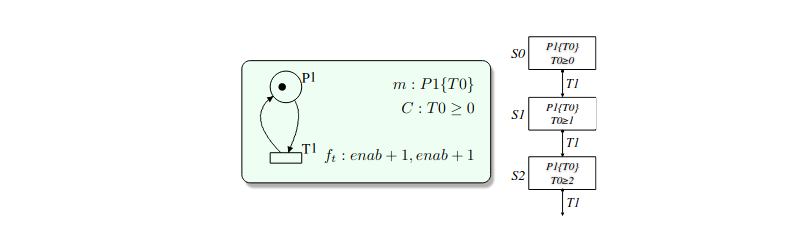
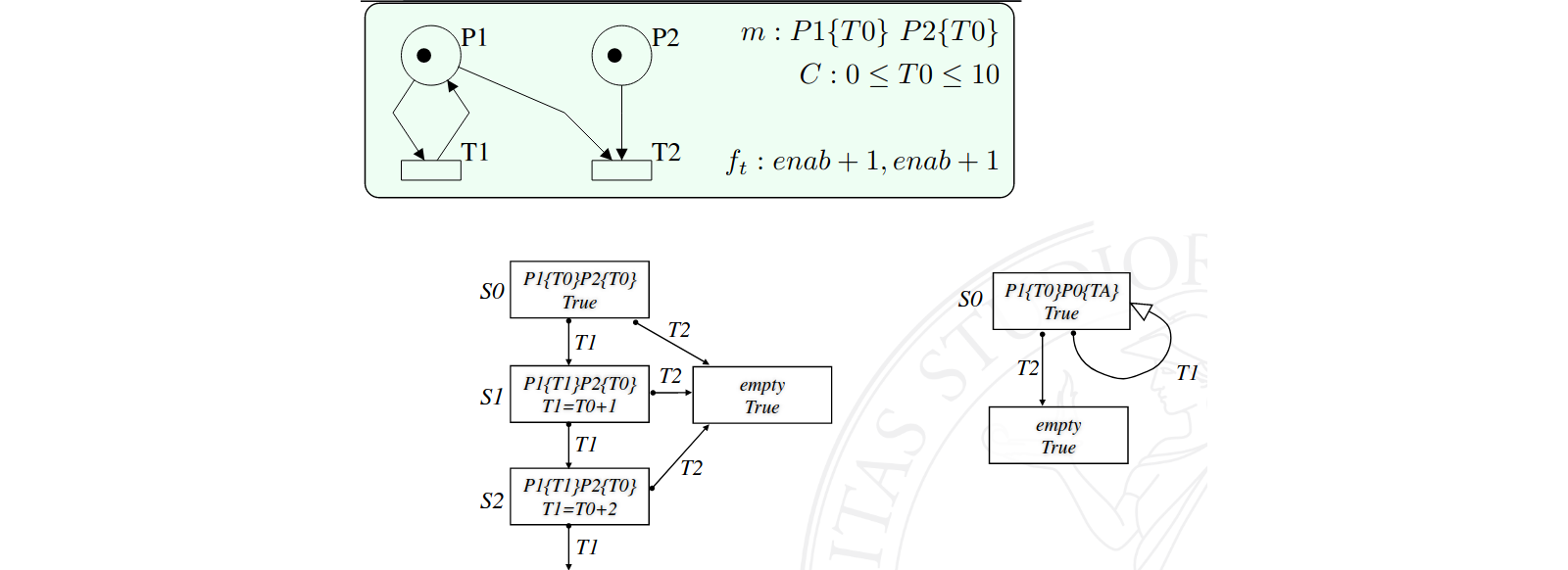
Osservando l’evoluzione di una rete Time Basic ci si può poi accorgere di un ulteriore fatto: se le funzioni temporali delle transizioni non fanno riferimento a tempi assoluti, ovvero a specifici istanti di esecuzione della rete, per comprendere come la rete può evolvere a partire da una certa marcatura è sufficiente osservare i vincoli relativi tra i timestamp.

Si prenda per esempio in considerazione la rete in figura:

ci si accorge che mantenere il riferimento ai tempi assoluti $0$ e $10$ introdotti dai vincoli iniziali farebbe sì che vengano generati infiniti stati anche considerando la possibilità di inclusione. Poiché l’unica transizione presente nella rete non fa alcun riferimento a tempi assoluti, si può quindi eliminare i vincoli legati a tempi assoluti ottenendo il secondo grafo in figura: esso rappresenta alla perfezione l’evoluzione della rete (che può far scattare la transizione $T1$ un numero infinito di volte) pur ignorando i vincoli sul valore iniziale del timestamp dell’unico gettone presente.

Tempi anonimi

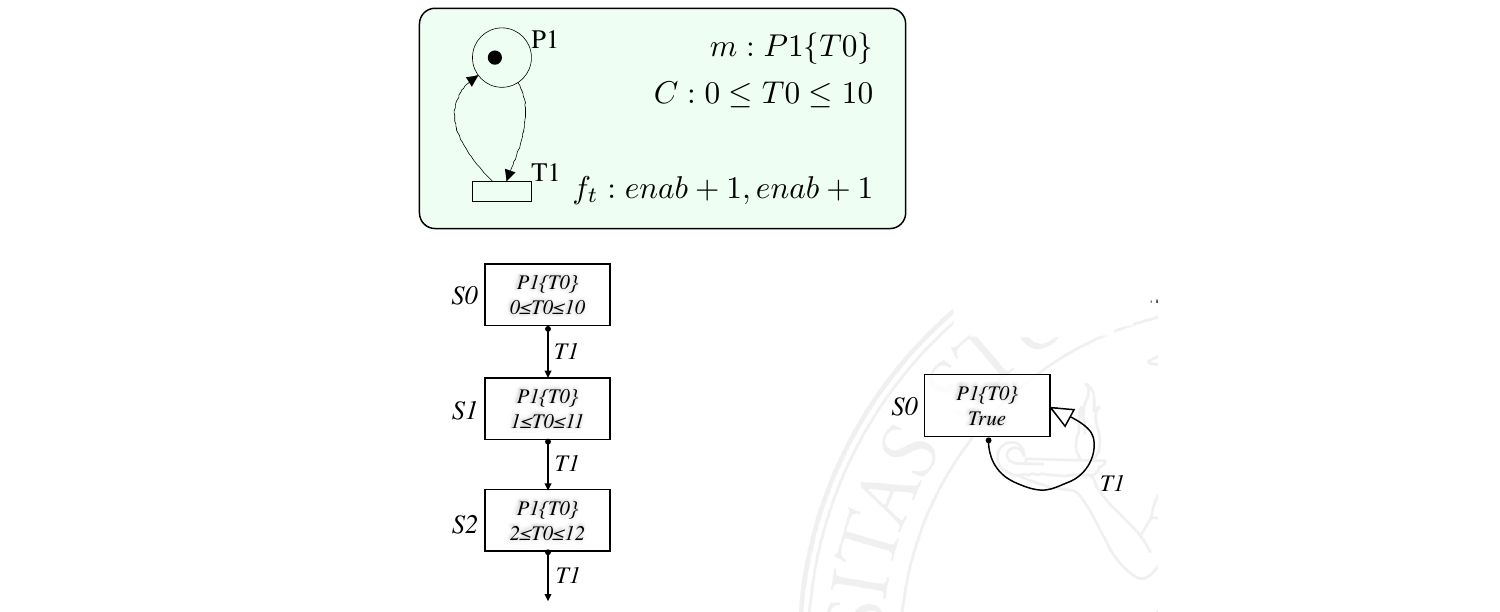
Si può infine introdurre un’ulteriore astrazione: ci si rende infatti conto che se il timestamp associato ad un gettone in una marcatura M non verrà mai più utilizzato per stabilire come evolverà la rete a partire da quella marcatura, allora è possibile anonimizzare il tempo di tale gettone. L’identificatore simbolico del gettone viene cioè sostituito da un identificatore anonimo $\tau_A$ e i vincoli che lo coinvolgono cancellati: questo permette di riconoscere la somiglianza tra stati simbolici che, pur diversi a livello di timestamp dei gettoni, evolvono nello stesso modo.

Si consideri per esempio la rete in figura:

All’interno di questa rete, il timestamp del gettone in $P2$ non ha alcuna influenza sull’evoluzione della rete: esso funge infatti unicamente da zero relativo per determinare il timestamp del gettone in $P1$, che sarà maggiore di esso di tante unità quanto il numero di volte che è scattata la transizione $T1$. Il gettone può dunque essere reso anonimo, eliminando l’unico vincolo che, a conti fatti, non aggiunge nulla alla nostra conoscenza della rete.

Non esiste una vera e propria regola formale per capire quali gettoni siano anonimizzabili, ma esistono una serie di euristiche che possono suggerire tale eventualità: così, per esempio, è molto probabile che i gettoni morti (gettoni in posti che non appartengono al preset di alcuna transizione) possano essere resi anonimi.

Conclusioni

L’utilizzo delle tecniche di raggruppamento degli stati simbolici appena viste permette di costruire dei grafi di raggiungibilità più coincisi per le reti Time Basic, ma non senza sacrificare una serie di informazioni. Infatti:

la tecnica di inclusione introduce la possibilità che nel grafo esistano dei cammini non percorribili dovuti al fatto che muovendosi tra sottoinsiemi degli stati rappresentati è possibile che lo stato simbolico reale in cui ci si trova non permetta una certa transizione che è invece possibile a parte degli stati rappresentati dal nodo;
con l’abolizione dei vincoli assoluti si perdono informazioni sulle relazioni precise tra gli stati (anche se è possibile arricchire le informazioni sugli archi per non perderne troppe);
anonimizzando alcuni gettoni potrebbe non essere sempre possibile verificare la raggiungibilità di una marcatura definita da vincoli sui timestamp.

Si tratta di un equo prezzo da pagare per una rappresentazione semplice ed efficace dell’evoluzione della rete.

Albero di copertura temporale?

Avevamo detto che sulle reti TB non era possibile utilizzare la tecnica di analisi di copertura vista per le normali reti di Petri a causa della distinguibilità tra gettoni dovuta ai rispettivi timestamp.

Tuttavia, l’introduzione della possibilità di anonimizzare i gettoni è in grado di far riconsiderare tale conclusione: i gettoni anonimi sono infatti tutti equivalenti e indistinguibili, motivo per cui potrebbero essere rappresentati globalmente solo dal loro numero $\omega_{\tau A}$.

Non approfondiamo la questione, ma esiste un’ipotesi non dimostrata che suppone che le reti TB non limitate siano non limitate solo sul numero di gettoni anonimi in quanto in caso contrario bisognerebbe avere una rete che si interessi del passato all’infinito.

Ingegneria del software