Controllori con specifica a stati proibiti
Tramite le reti di Petri si possono modellare dei controllori che forzano o limitano certi comportamenti del sistema: se si desidera cioè che la rete rispetti una certa invariante si introduce un controllare che la forzi. Controllare significa assicurarsi che vengano rispettate certe proprietà.
È possibile definire gli stati come situazioni che si possono verificare, e le transizioni come eventi che si verificano. Lo scopo è controllare che le transizioni possano svolgere certe operazioni, oppure no.
Esistono due classi di problemi che limitano la capacità espressiva dei controllori:
- non tutte le transizioni sono osservabili: il controllore non ne ha le capacità, oppure è un’attività troppo onerosa;
- l’osservazione di alcune situazioni ne comporta il cambiamento.
Inoltre, non tutto è controllabile: non si può chiedere ad una centrale nucleare in surriscaldamento di non esplodere, ma si possono attivare i sistemi di sicurezza.
Nel modello del controllore a stati proibiti, l’attività di controllo si traduce formalmente in una combinazione lineare delle marcature che deve rimanere sotto una certa soglia.
Si vincola quindi per un sottoinsieme di posti che la combinazione lineare di una marcatura \(M\) con un vettore dei pesi \(L\) sia minore o uguale (e non solo uguale come nei \(P\)-invarianti) di una soglia data:
$$ LM \leq b. $$
Come abbiamo visto nel corso di Ricerca Operativa, è sempre possibile riportare un sistema di disequazioni ad un sistema di equazioni inserendo variabili aggiuntive (slack) semipositive:
$$ LM + x = b \: \vert \: x \geq 0. $$
Mutua esclusione
Il problema della mutua esclusione è l’accesso esclusivo a zona critica da parte di più soggetti. Nel seguente esempio si vuole imporre che non sia possibile avere gettoni contemporaneamente in \(P_1\) e \(P_3\).
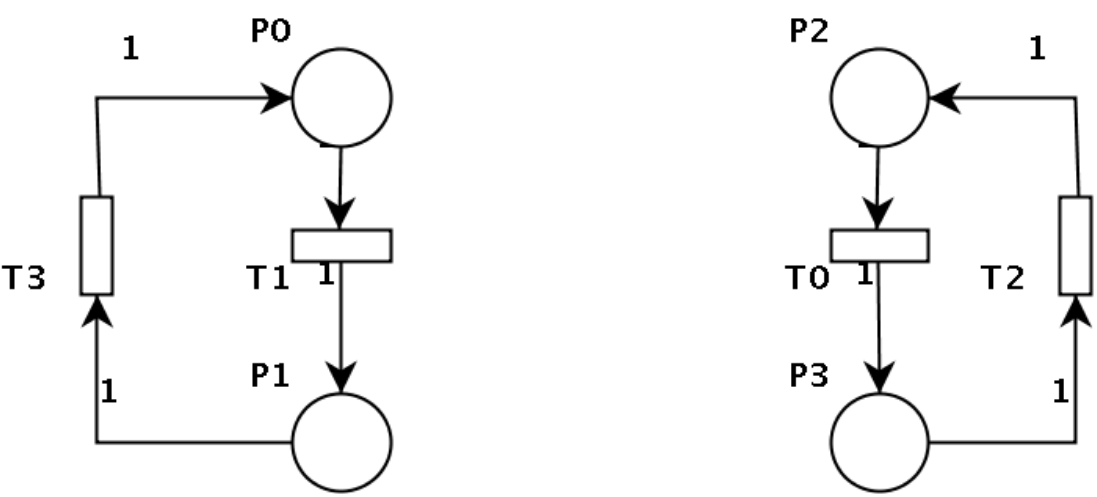
Matematicamente il vincolo si può esprimere con la seguente disequazione.
$$ P_1 + P_3 \leq 1 $$
La tecnica del controllore a stati proibiti aggiunge tanti posti di controllo quanti sono il numero di disequazioni (e quindi il numero di variabili di slack) per modificare il comportamento delle transizioni.
In questo caso, per trasformare la disequazione in un’equazione si aggiunge una variabile di slack, rappresentante il nuovo posto controllore \(P_c\).
$$ P_1 + P_3 + P_c = 1 $$
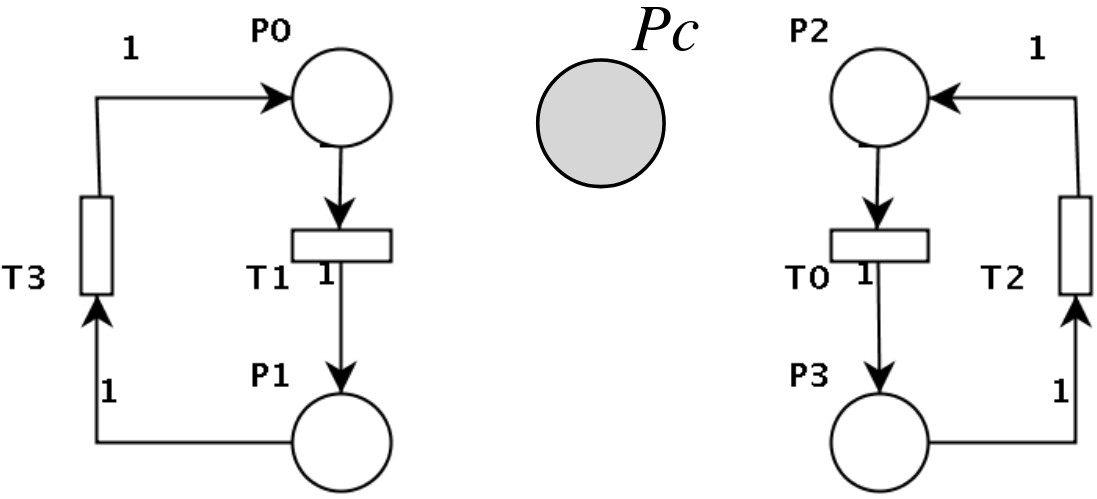
Per collegare \(P_c\) alle diverse transizioni occorre aggiungere una riga \(C_c\) nella matrice di incidenza \(C_s\):
$$ C_\text{nuova} = \begin{bmatrix} C_s \\ C_c \end{bmatrix}. $$
Inoltre, bisogna aggiungere la marcatura iniziale \(M_{0c}\) del posto \(P_c\) alla marcatura iniziale del sistema \(M_{0s}\):
$$ M_{0} = \begin{bmatrix} M_{0s} \\ M_{0c} \end{bmatrix}. $$
Riscrivendo quindi il vincolo tramite le matrici otteniamo:
$$ LM_s + M_c = b. $$
Sia \(\begin{bmatrix} L I\end{bmatrix}\) la giustapposizione tra \(L\) e la matrice identità \(I\) e \(M\) la giustapposizione di \(M_s\) e \(M_c\), allora:
$$ \begin{bmatrix} L I \end{bmatrix} M = b. $$
L’espressione sopra ricorda la definizione di \(P\)-invariante (\(hm = 0\)). Volendo forzare che \([L I]\) sia un’invariante, riprendiamo quindi la relativa definizione:
$$ \begin{bmatrix} L I \end{bmatrix} C = 0, $$
che, rifacendosi al vincolo originale, si può a sua volta riscrivere come
$$ L C_s + I C_c = 0 \\ \boxed{C_c = -LC_s}. $$
Le righe da aggiungere al sistema \(C_c\) sono quindi uguali a \(-LC_s\), dove:
- \(C_s\) è la matrice di incidenza del sistema originale;
- \(L\) è il vincolo desiderato, fissato;
- \(C_c\) la si trova con un semplice calcolo matriciale.
Sintesi del controllore
Continuando l’esempio precedente, l’obiettivo è trovare
$$ \begin{align*} C_s &= \begin{bmatrix} 0 &-1 &0 &1 \\ 0 &1 &0 &-1 \\ -1 &0 &1 &0 \\ 1 &0 &-1 &0 \end{bmatrix} \quad L = \begin{bmatrix} 0 &1 &0 &1 \end{bmatrix} \\ -LC_s &= \begin{bmatrix} -1 &-1 & \phantom{-} 1 & \phantom{-} 1 \end{bmatrix}. \end{align*} $$
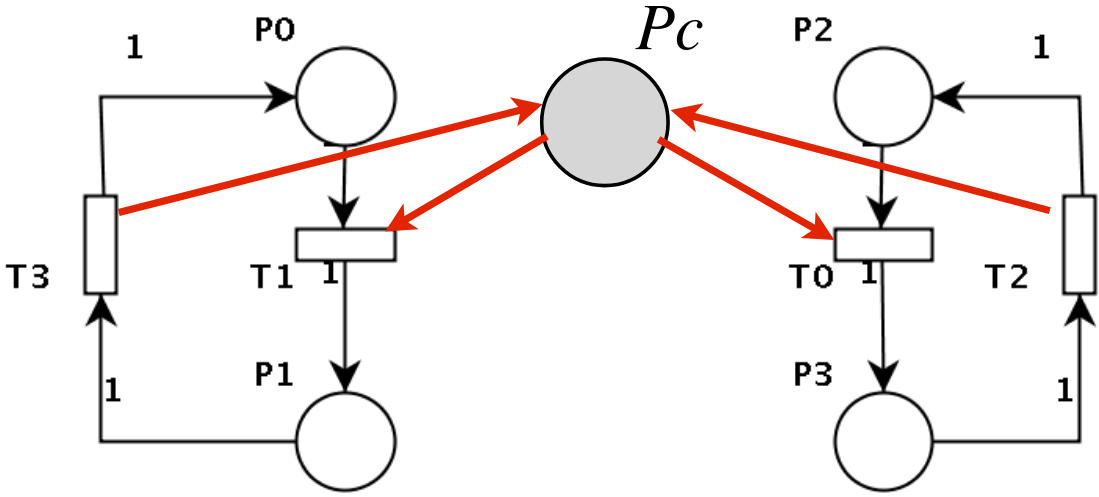
Il vettore \(-LC_s\) definisce gli archi in ingresso e in uscita dalle transizioni per il posto controllore \(P_c\):
il posto ha in ingresso \(T_0\) e \(T_1\) (gli elementi con -1) mentre in uscita \(T_2\) e \(T_3\) (gli elementi con 1).
Da questi risultati è possibile ottenere anche la marcatura iniziale del posto controllore (\(M_{0_c}\)):
$$ LM_{0s} + M_{0c} = b \\ \boxed{M_{0c} = b - LM_{0s}}. $$
Essendo tutti termini noti, è facile rispondere che la marcatura iniziale di \(P_c\) è uguale a 1.
In conclusione, le due formule principali da conoscere sono le seguenti:
- \(\boxed{C_c = -LC_s}\) per calcolare le righe da aggiungere alla matrice di incidenza \(C_s\);
- \(\boxed{M_{0c} = b - LM_{0s}}\) per calcolare la marcatura iniziale del posto controllore \(P_c\).
Esempio
Riprendendo il classico esempio dei lettori e scrittori, lo scopo di questo esercizio è collegare le due parti assicurando l’accesso esclusivo alla risorsa.
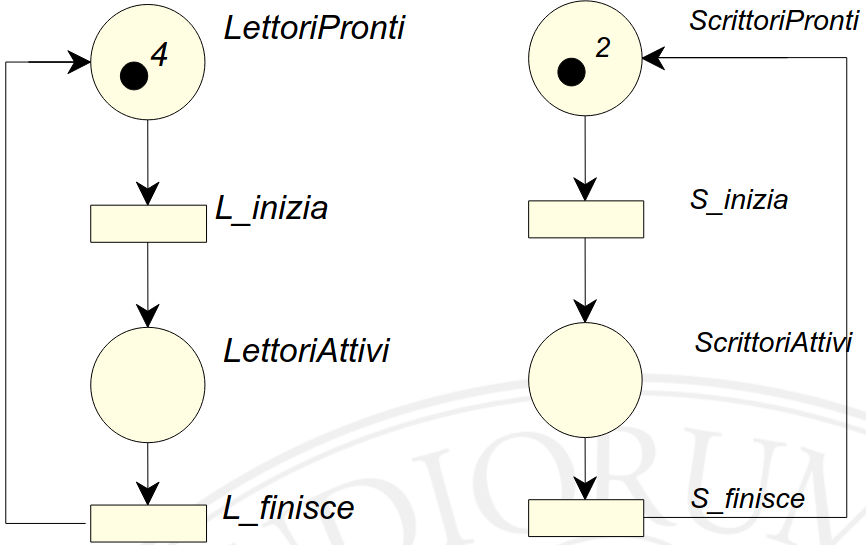
Dovendo imporre la mutua esclusione tra lettori e scrittori, poniamo i seguenti vincoli:
$$ \begin{cases} \text{LettoriAttivi} + \text{ScrittoriAttivi} \leq 1 \\ \text{LettoriAttivi} + 4 \cdot \text{ScrittoriAttivi} \leq 4 . \end{cases} $$
Il primo vincolo è incluso nel secondo, quindi possiamo ignorarlo.
Date le seguenti informazioni, possiamo realizzare nella rete i vincoli sopra.
$$ M_0 = \begin{bmatrix} 4 &0 &2 &0 \end{bmatrix}, \quad C = \begin{bmatrix} -1 &1 &0 &0 \\ 1 &-1 &0 &0 \\ 0 &0 &1 &-1 \\ 0 &0 &-1 &1 \end{bmatrix} \tag{Dati della rete} $$ $$ LM \leq b \tag{Vincolo} $$ $$ L = \begin{bmatrix} 0 &1 &0 &4 \end{bmatrix} \quad b = 4 \tag{Parametri del vincolo} $$
È sufficiente quindi sfruttare le formule viste prima per trovare la nuova riga della matrice di incidenza e la marcatura iniziale di \(P_0\).
$$ \begin{align} C_c = -LC_s &= \begin{bmatrix} -1 &1 &4 &-4 \end{bmatrix} \\ M_{0_c} = b - LM_{0_s} &= 4. \end{align} $$