Albero di copertura

A questo punto risulterà normale chiedersi se sia possibile creare una struttura dati (albero e grafo) anche per le reti illimitate, cui nodi rappresenteranno gruppi di stati potenzialmente infiniti.
È bene introdurre il concetto di copertura prima di procedere.

Una marcatura $M$ copre una marcatura $M’$ se e solo se:

$$ \forall p \in P \quad M(p) \geq M’(p). $$

Ovvero se per ogni posto in $P$, la marcatura $M(p)$ è maggiore o uguale a $M’(p)$.

Al contrario, $M$ si dice copribile da $M’$ se e solo se:

$$ \exists M\smash{‘’} \! \in R(M’) \: \vert \: M’’ \! \textit{ copre } M. $$

Grazie al concetto di copertura è possibile ridefinire quello di transizione morte:
una transizione $t$ si dice morta se e solo se data la sua marcatura minima $M$ (ovvero il minor numero di gettoni necessario in ogni posto nel suo preset per abilitarla) questa non è copribile a partire dalla marcatura corrente. In caso contrario la transizione $t$ è almeno 1-viva.

Si conclude quindi che se una marcatura ne copre un’altra, tutte le azioni possibili nella prima sono possibili anche nella seconda. È quindi possibile modificare l’albero di raggiungibilità in modo tale che, quando viene creato un nodo è necessario verificare se tra i suoi predecessori ne esiste uno che lo copre, allora a questo punto nei posti dove c’è copertura propria (ovvero $M(p) \geq M’(p)$) si mette $\omega$.
Il simbolo $\omega$ rappresenta un numero grande a piacere (e non qualsiasi), che può aumentare all’infinito: questo aspetto è da tenere in considerazione quando bisogna cercare quali transizioni sono abilitate da esso. Questo tipo di notazione ($\omega$) viene introdotta per limitare l’aumento spropositato di nodi nel diagramma, comprimendo marcature uguali se non per $\omega$.

Se una marcatura $M$ copre una precedente $M’$, infatti, è possibile ripetere gli scatti delle transizioni in $M’$ per arrivare ad $M$; se al termine di questa operazione sono presenti più gettoni in un posto, allora è possibile crearne un numero grande a piacere.

È importante notare come le transizioni che erano abilitate in una certa marcatura $M’$ lo saranno anche in una marcatura diversa che copre $M’$, a meno che non ci siano archi inibitori.

È ora possibile definire l’algoritmo per la creazione di un albero di copertura, comunque simile in molti punti al precedente:

crea la radice dell’albero corrispondente alla marcatura iniziale $M_0$ ed etichettala come nuova;
finché esistono nodi etichettati come “nuovi” esegui:
1. seleziona una marcatura $M$ etichettata come “nuova”;
  prendila in considerazione e rimuovi l’etichetta “nuova”.
2. se la marcatura $M$ è identica ad una marcatura di un altro nodo allora:
  - etichetta $M$ come “duplicata”;
  - continua passando alla prossima iterazione.
3. se nella marcatura $M$ non è abilitata nessuna transizione allora:
  - etichetta $M$ come “finale”;
  altrimenti esegui:
  - finché esistono transizioni abilitate in $M$ esegui:
    - per ogni transizione $t$ abilitata in $M$ esegui:
      1. crea la marcatura $M’$ prodotta dallo scatto di $t$;
      2. se sul cammino dalla radice ($M_0$) alla marcatura $M$
        esiste una marcatura $M’‘$ coperta da $M’$ allora
        
        aggiungi $\omega$ in tutte le posizioni corrispondenti a coperture proprie;
      3. crea un nuovo nodo corrispondente alla marcatura $M’$;
      4. aggiungi un arco nell’albero al nodo corrispondente di $M$ al nodo di $M’$;
      5. etichetta la marcatura $M’$ come “nuova”.

Dall’albero generato da questo algoritmo è possibile arrivare al grafo di copertura.

Inoltre, ripetendo l’algoritmo precedente su una rete limitata viene generato un grafo di copertura senza $\omega$ e quindi equivalente a un albero di raggiungibilità.

L’algoritmo termina in ogni caso: è sufficiente osservare l’albero risultante per stabilire se la rete considerata è limitata oppure no.

Esempio

Partendo dalla rete di Petri sottostante ed applicando l’algoritmo appena descritto è possibile arrivare ad un albero di copertura.

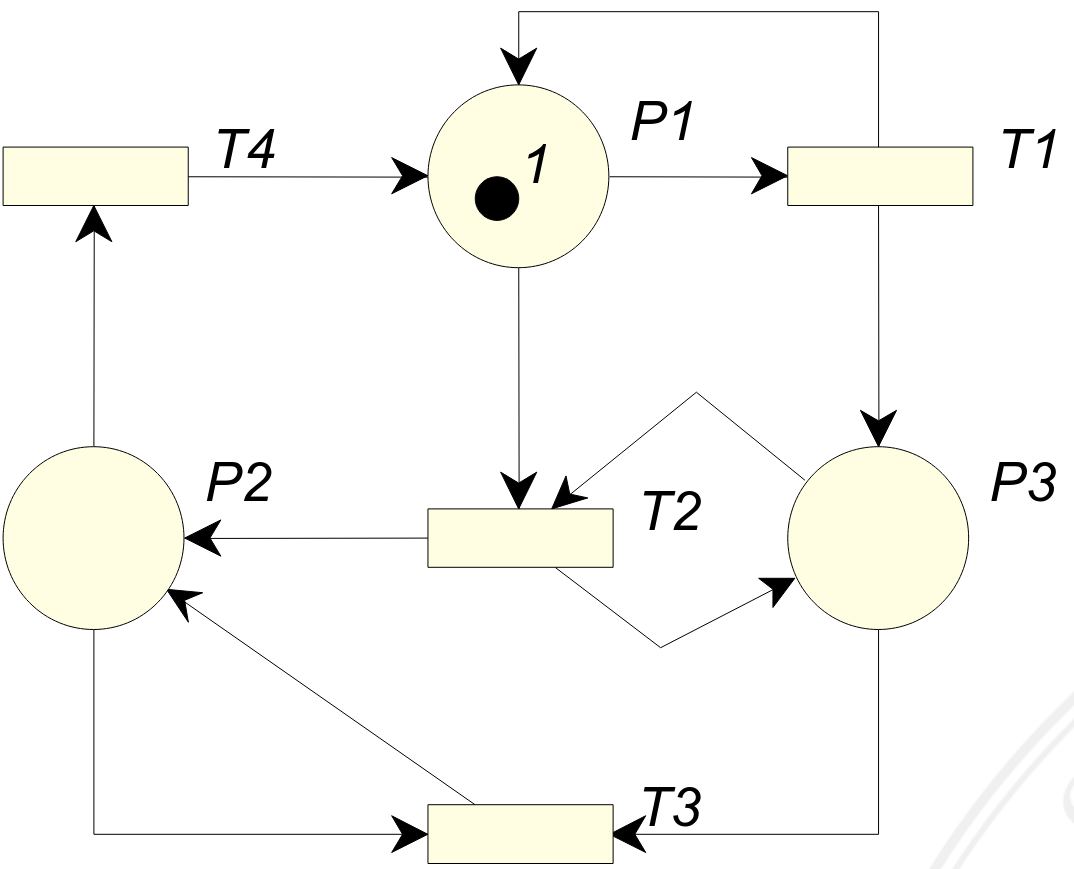
Come visto nell’esempio della creazione di un albero di raggiungibilità, il primo passo da fare è creare il nodo radice corrispondente alla marcatura iniziale ($\nodenew{100}$) e marcarlo come nuovo.
Successivamente, è necessario considerare l’unico nodo esistente ($\node{100}$) e iterare tra le sue transizioni. In questo caso, è abilitata la transizione $t_1$ che porta a una marcatura $M’ = \nodenew{101}$.

A questo punto si può notare come la radice sia una marcatura coperta da $M’$, in quanto:

$M \: \vert \: 1 \geq 1 \: \vert \: M’$;
$M \: \vert \: 0\geq 0 \: \vert \: M’$;
$M \: \vert \: 1 > 0 \: \vert \: M’$.

Nel nodo corrispondente alla marcatura $M’$ è quindi possibile sostituire l’unica copertura propria (quella con il $>$ e non il $\geq$) con il simbolo $\omega$ e marcare il nodo. Questa è l’unica parte dell’algoritmo differente da quello che genera l’albero di raggiungibilità: il resto dell’esempio è quindi completato dall’immagine sottostante.

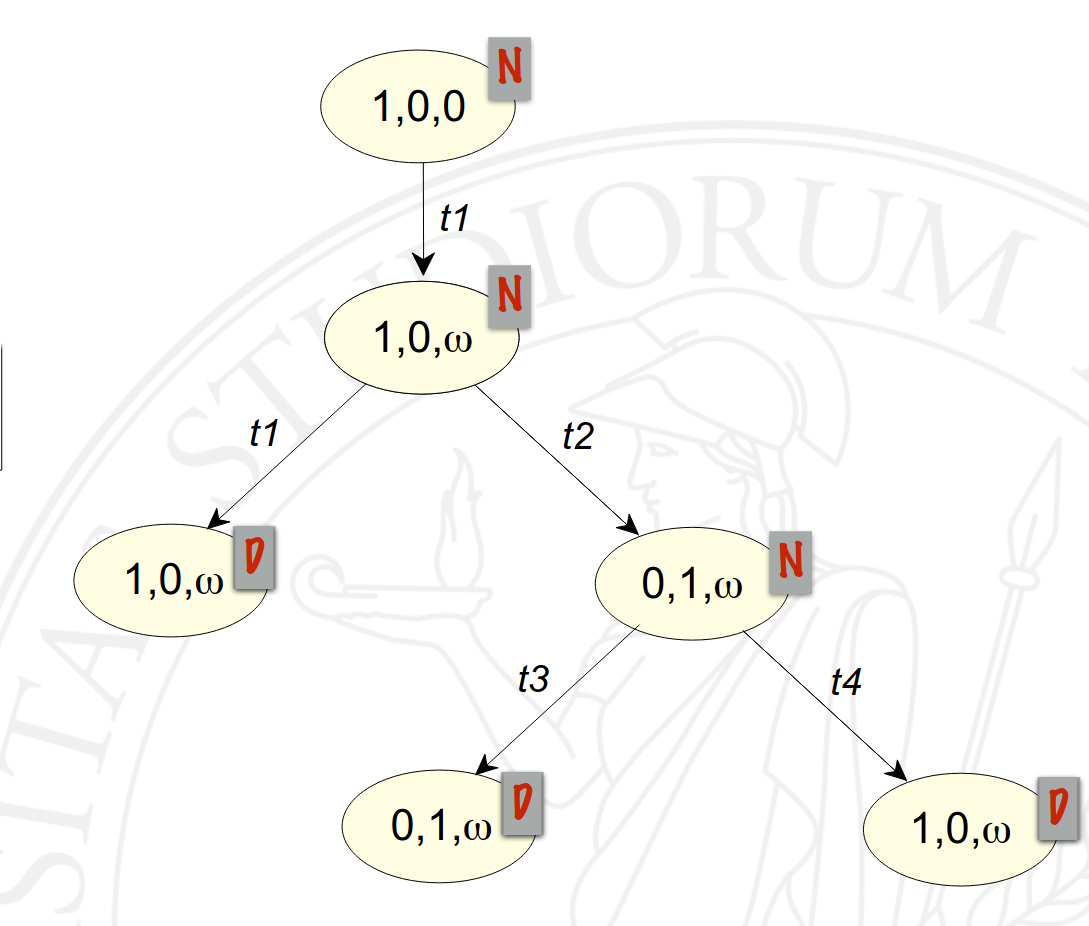
Tramite lo stesso procedimento attuato per gli alberi di raggiungibilità, è possibile trasformare il precedente albero in un grafo di copertura.

Considerazioni

se $\omega$ non compare mai nell’albero di copertura la rete è limitata;
una rete di Petri è binaria se nell’albero di copertura compaiono solo 0 e 1;
una transizione è morta (0-viva) se non compare mai come etichetta di un arco dell’albero di copertura;
condizione necessaria affinché una marcatura $M$ sia raggiungibile è l’esistenza di un nodo etichettato con una marcatura che copre $M$ (non sufficiente: le marcature coperte non sono necessariamente raggiungibili);
non è possibile stabilire se una rete è viva.

Esempio particolare

È doveroso un ulteriore esempio particolare nel caso di reti non vive.
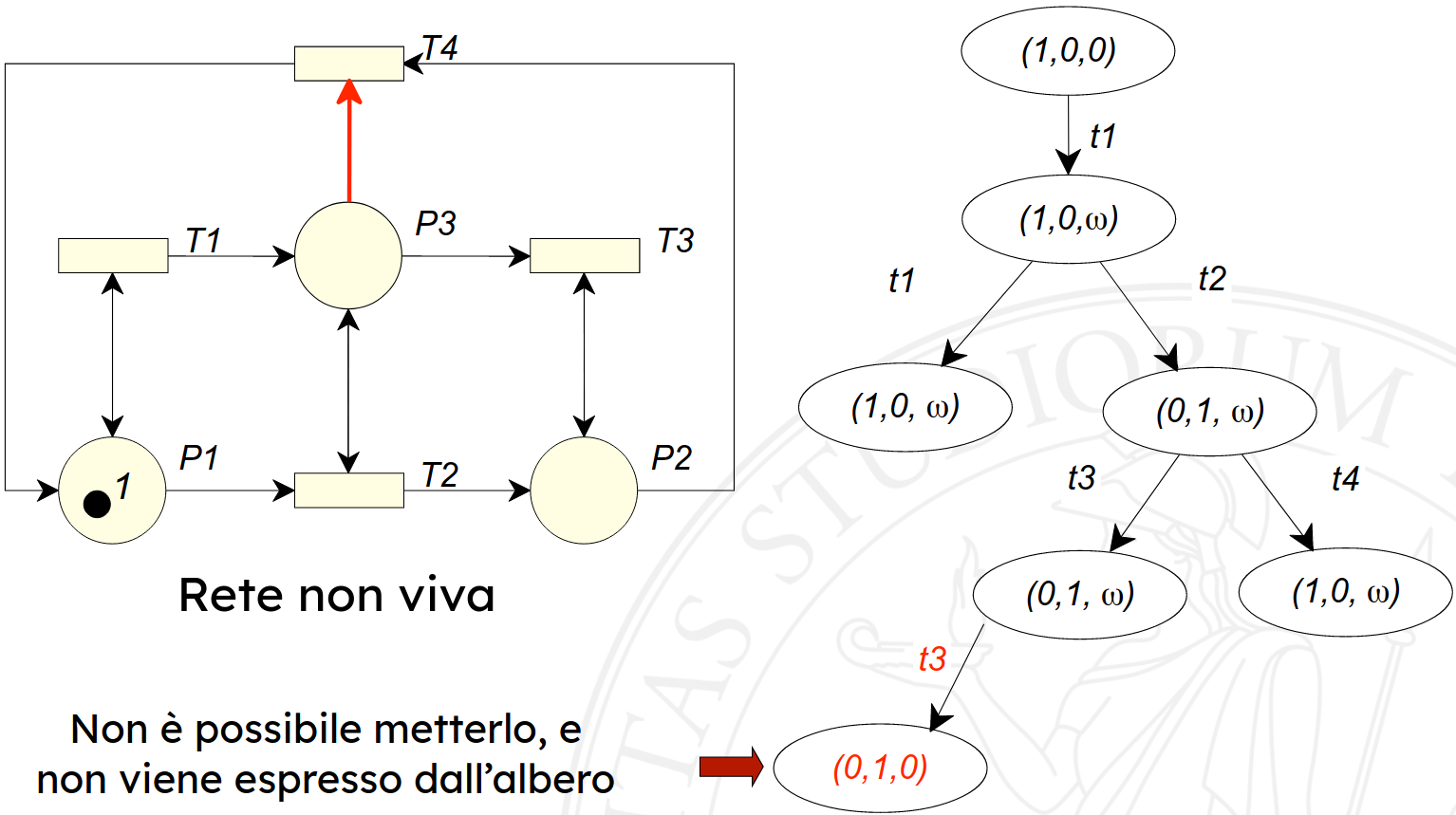
Data una rete non viva (come nella figura sotto) dall’albero di copertura non è possibile evincere se la rete è effettivamente viva o no: infatti se il nodo $\node{01$\omega$}$ è duplicato, quindi non verrà più espanso. A questo punto non è possibile aggiungere all’interno dell’albero il nodo $\node{010}$, in cui la rete raggiunge un deadlock. Questo però significa che questo albero di copertura è uguale a quello della stessa rete senza arco che collega $p_3$ a $t_4$, che in quel caso è una rete viva. Detto ciò si può affermare che tramite l’albero di copertura non è possibile dire se una rete è viva oppure no.

Da albero di copertura a rete

Passare dall’albero di copertura alla rete di Petri è un’operazione che rispetto all’inverso crea più incertezza. L’albero di copertura permette infatti di rappresentare reti potenzialmente illimitate, è quindi normale avere come risultato reti di cui non si conosce la struttura: molte reti potrebbero essere associate allo stesso albero.

Nel seguente esempio si può notare come la rete ricavata presenta degli archi tratteggiati: potrebbero essere presenti, oppure no. Inoltre, sono assenti anche i pesi negli archi. Tale mancanza di informazioni è dovuta in gran parte dalla presenza di $\omega$: un nodo con all’interno $\omega$ rappresenta diverse marcature.

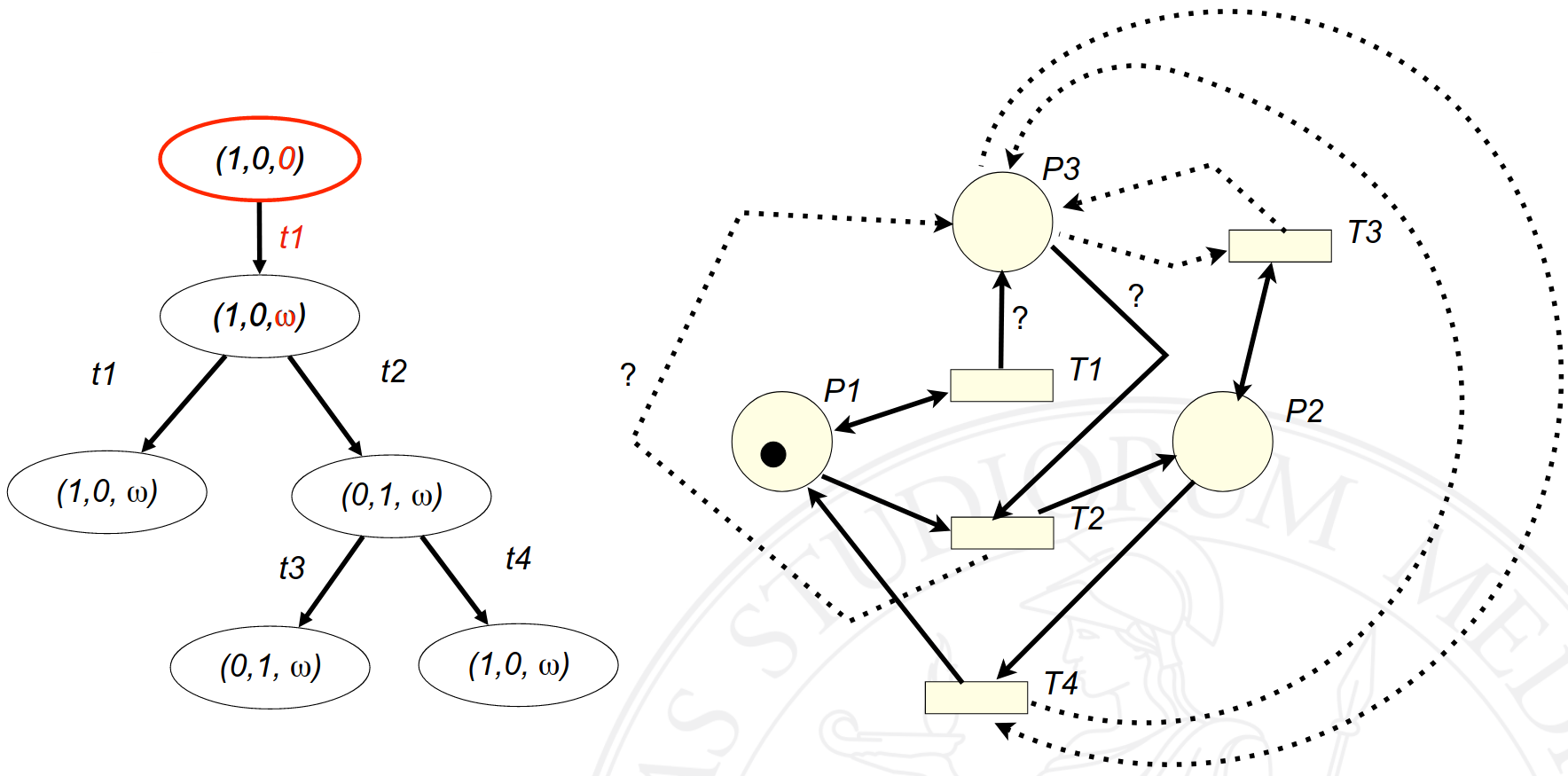
È importante notare come le marcature sicuramente raggiungibili siano quelle i cui nodi nell’albero di copertura non contengono $\omega$: delle altre non si può essere certi.

Ingegneria del software

Albero di copertura

Esempio

Considerazioni

Esempio particolare

Da albero di copertura a rete