Modelli temporali

Esistono una serie di proposte per modellare il concetto di tempo (deterministico) all’interno delle reti di Petri. Esse si dividono sostanzialmente in due grandi categorie:

• quelle che introducono ritardi sui posti;
• quelle che introducono ritardi sulle transizioni.

Tempo sui posti

Il tempo associato a ciascun posto rappresenta il tempo che un gettone deve rimanere in tale posto prima di essere considerato per l’abilitazione di transizioni che hanno tale posto nel proprio preset.

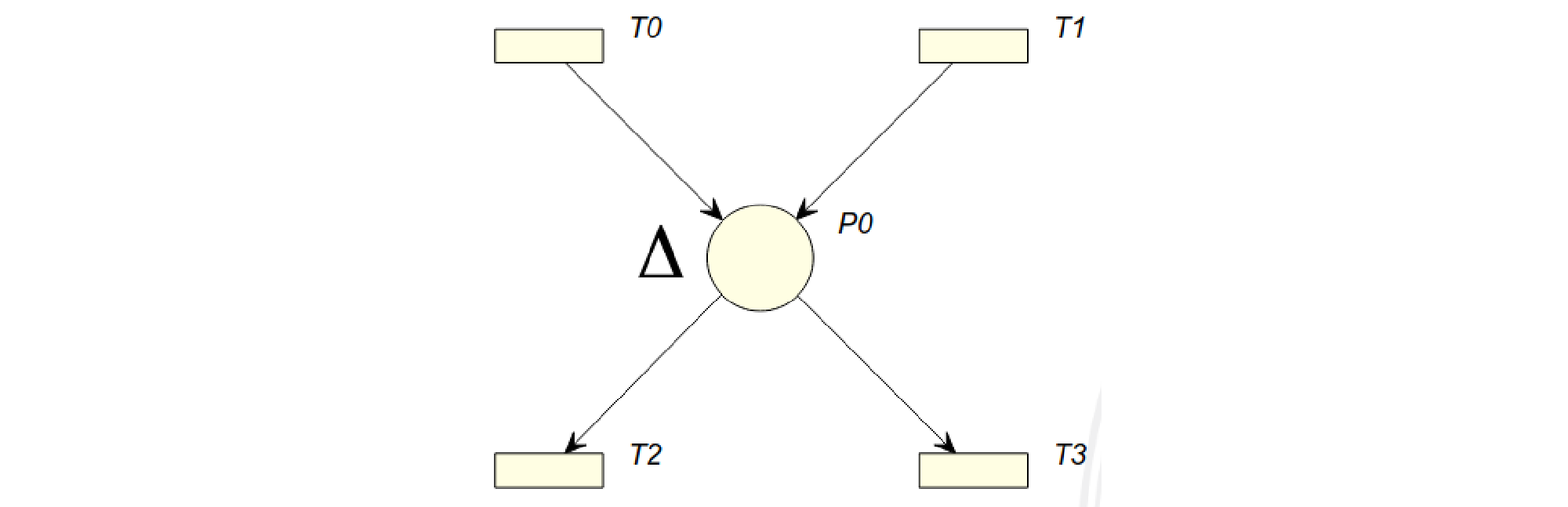
Dopo lo scatto di una transizione i gettoni generati in un posto non fanno cioè funzionalmente parte della sua marcatura prima che sia passato un dato intervallo di tempo \(\Delta\). Tale \(\Delta\) può quindi essere considerato la durata minima di permanenza del gettone in tale posto, bloccando così quella porzione di stato del sistema per un certo periodo.

Tempo sulle transizioni

Quando si associa un tempo ad una transizione è bene indicare che cosa esso rappresenti. Il tempo di una transizione può infatti rappresentare due concetti molto differenti:

• la durata della transizione, ovvero il tempo richiesto dopo lo scatto della transizione perché vengano generati i gettoni nel suo postset (una sorta di ritardo di scatto);
• il momento dello scatto della transizione, che può essere espresso in modo diverso a seconda del modello.

Esistono a dire il vero anche modelli misti che permettono di specificare sia la durata di una transizione che il suo tempo di scatto.

Equivalenza tra tempi sui posti e sulle transizioni

È facile dimostrare che sia le reti che definiscono tempi sui posti che quelle che definiscono tempi sulle transizioni, sia come durata che come momento dello scatto, sono funzionalmente equivalenti, ovvero permettono di rappresentare lo stesso insieme di sistemi.

Ciò è testimoniato dal fatto che, come mostra la figura sottostante, ogni rete avente tempo sui posti può essere trasformata in una rete con durata delle transizioni semplicemente aggiungendo una transizione di “ritardo” e separando il posto in due. Ovviamente vale anche il viceversa.

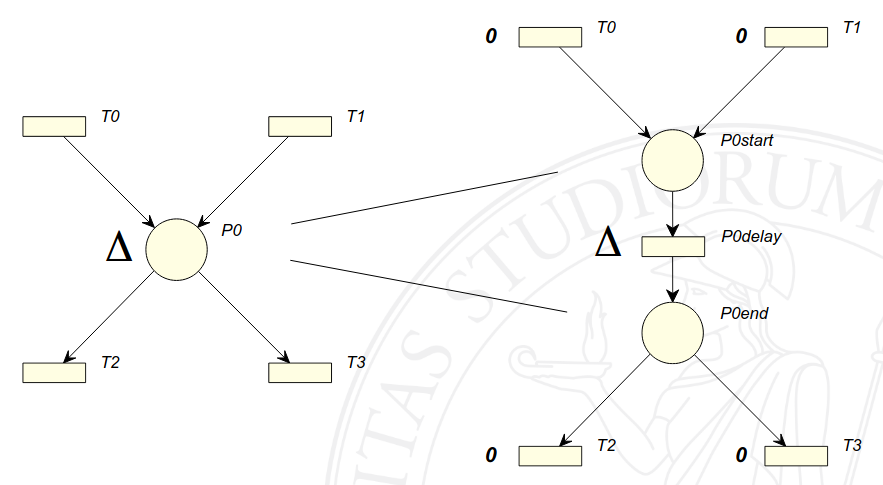
Similmente, reti con durata delle transizioni possono essere trasformate in reti con tempi di scatto per le transizioni modellando esplicitamente con un posto il ritardo con cui vengono generati gettoni nel postset della transizione originale.

Tempi di scatto

Ritornando un attimo sui nostri passi, diamo ora un’occhiata migliore a come si possono definire i tempi di scatto di una transizione.

Nella definizione dei tempi di scatto delle transizioni esistono infatti una serie di alternative molto differenti. Innanzitutto, i tempi possono essere:

• unici, ovvero ogni transizione scatta (o può scattare) in uno e un solo specifico momento;
• multipli, ovvero ogni transizione scatta (o può scattare) in uno in un insieme di momenti. A seconda del modello considerato tali insiemi possono essere veri e propri insiemi matematici (es. reti TB) oppure intervalli.

Si noti come i primi possono essere visti come casi particolari dei secondi.
Considerando ciò, gli insiemi (anche unitari) di tempi di scatto si distinguono poi in due categorie:

• insiemi costanti, ovvero tali per cui l’insieme dei tempi di scatto è definito staticamente ed è sempre uguale indipendentemente dall’evoluzione della rete;
• insiemi variabili, ovvero tali per cui l’insieme dei tempi di scatto può variare dinamicamente in base allo stato della rete o a porzioni di esso (es. reti TB e HLTPN).

Anche in questo caso i primi possono essere visti come un caso particolare dei secondi, in cui cioè l’insieme potrebbe variare ma non varia mai.
Infine, i tempi di scatto stessi possono essere divisi in base a come vengono definiti:

• tempi relativi, ovvero espressi solo in termini relativi al tempo di abilitazione della transizione (es. “2 ms dopo l’abilitazione”);
• tempi assoluti, ovvero espressi in termini relativi a tempi assoluti e ai tempi associati ai gettoni che compongono l’abilitazione (es. “dopo 3 minuti dall’avvio del sistema” o “dopo 4 ms dal tempo associato all’ultimo gettone nell’abilitazione”) (es. reti TBe TCP).

Nuovamente, i primi possono essere visti come un sottoinsieme dei secondi.

Tutto questo insieme di variabili permette di definire reti temporizzate basate su tempi di scatto delle transizioni anche molto diverse tra di loro. Avremo per esempio le reti Time Petri, che utilizzano tempi di scatto relativi, multipli e a intervalli costanti; le reti Time Petri colorate, simili alle precedenti ma che usano tempi assoluti; le reti Time Petri ad alto livello, che usano insiemi variabili, e molte altre.

Tra tutte queste tipologie, tuttavia, ci concentreremo sulle reti Time Basic. In virtù delle inclusioni di cui abbiamo già detto tali reti saranno quindi le più generali possibile e, dunque, anche le più interessanti.