Rappresentazione matriciale
Prima di procedere con la spiegazione delle tecniche di analisi statiche, è necessario introdurre una nuovo modo per rappresentare le reti di Petri: la rappresentazione matriciale. Essendo tutte rappresentazioni formali, non ambigue e complete, data una qualsiasi rete rappresentata graficamente o in forma logica, è possibile trasformarla automaticamente in una rete in forma matriciale, e viceversa.
Il vantaggio principale della rappresentazione matriciale è la maggiore semplicità ed efficienza nel trattamento matematico delle reti.
Le matrici che verranno utilizzate sono diverse, tra cui:
- \(I\): rappresenta gli archi in ingresso, ovvero le coppie di flusso che da un posto vanno nelle transizioni;
- \(O\): rappresenta gli archi in uscita, ovvero le coppie di flusso che da una transizione vanno nei posti;
- vettore \(m\): rappresenta la marcatura dei posti.
Definizione parte statica
Matrici \(I\) e \(O\)
Diversamente dalla rappresentazione logica in cui venivano utilizzati degli indicatori alfanumerici per riferirsi ai posti e alle transizioni, nella rappresentazione matriciale viene assegnato un indice ad ogni posto e ad ogni transizione. Ogni indice deve essere possibilmente continuo (senza salti) e biunivoco: ogni indice corrisponde ad un posto e ogni posto corrisponde ad un indice.
- indice dei posti: \(p: 1..\vert P \vert \rightarrow P\)
- indice delle transizioni: \(t: 1..\vert T \vert \rightarrow T\)
La dimensione delle due matrici è \(\vert P \vert \times \vert T \vert\): la cardinalità dei posti corrisponde al numero di righe e il numero delle transizioni corrisponde al numero delle colonne.
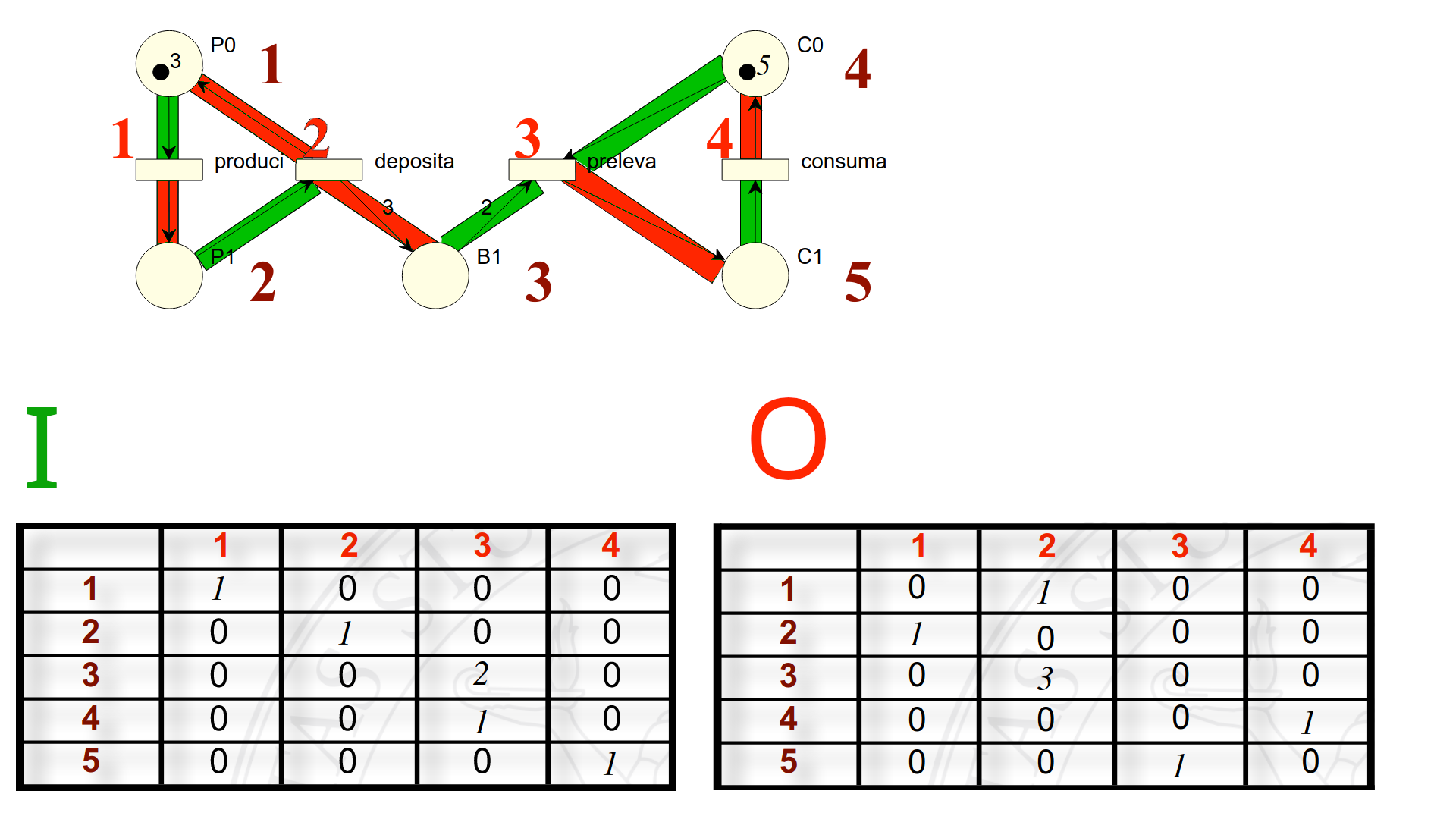
Per ogni flusso uscente dal posto \(i\)-esimo ed entrate nella transizione \(j\)-esima, l’elemento \(I[i][j]\) equivale al peso di tale flusso, oppure \(0\) se il flusso non esiste. In sintesi:
$$ \forall i \in 1..\vert P \vert , \, \forall j \in 1..\vert T \vert \quad I[i][j] = \begin{cases} W(\langle p(i), \, t(j) \rangle) &\text{se} \ \langle p(i), \, t(j) \rangle \in F, \ 0 &\text{altrimenti}. \end{cases} $$
Analogamente, per la matrice degli output \(O\):
$$ \forall i \in 1..\vert P \vert , \, \forall j \in 1..\vert T \vert \quad O[i][j] = \begin{cases} W(\langle t(j), \, p(i) \rangle) &\text{se} \ \langle t(j), \, p(i) \rangle \in F, \ 0 &\text{altrimenti}. \end{cases} $$
Per indicare il vettore colonna \(k\) da una matrice \(X\) spesso verrà utilizzata la notazione \(X[.][k]\).
Marcatura \(m\)
Per ogni posto, il vettore \(m\) di dimensione \(\vert P \vert\) indica la marcatura corrente.
$$ \forall i \in 1..\vert P \vert \quad m[i] = M(p(i)) $$
Che differenza c’è tra il vettore \(m\) e \(M\)? Entrambi logicamente indicano la stessa cosa, ma:
- gli indici di \(m\) sono nell’insieme \(1..\vert P \vert\);
- gli indici di \(M\) sono nell’insieme \(P\).
Definizione parte dinamica
Abilitazione di una transizione
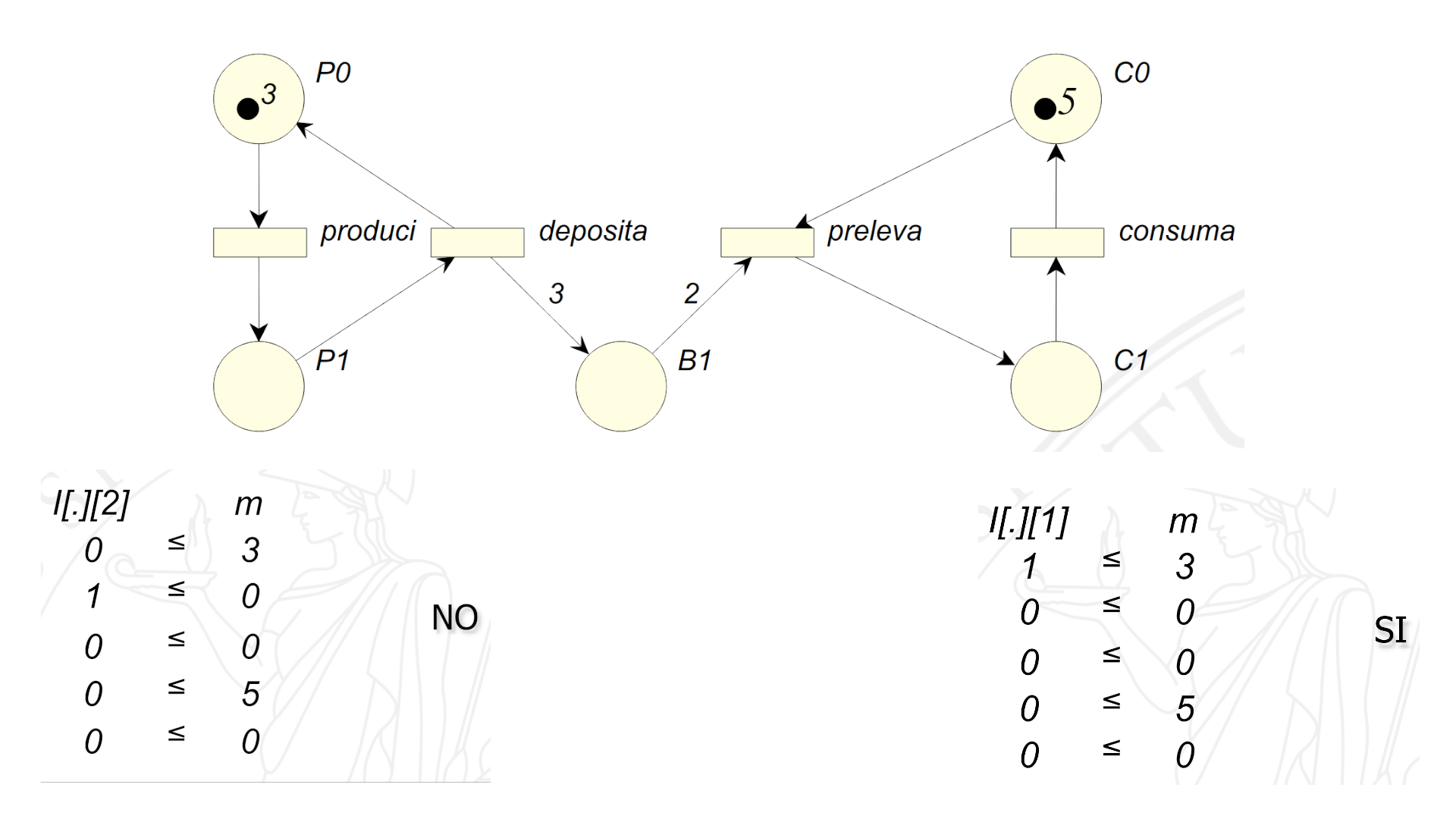
La transizione \(j\)-esima è abilitata in una marcatura (espressa dal vettore \(m\)) se e solo se il vettore colonna della sua matrice di input \(I[.][j]\) è minore o uguale alla marcatura corrente \(m\):
$$ \boxed{m \ [ \ t (j) >} \Longleftrightarrow I[.][j] \leq m \\ \textit{o se proprio vogliamo essere precisi…} \\ \boxed{m \ [ \ t(j) >} \Longleftrightarrow \forall i \in 1..\vert P \vert \quad I[i][j] \leq m[i]. $$
In sostanza, si controlla che il numero dei gettoni di ogni posto \(p(i)\) del preset sia maggiore o uguale del peso dell’arco che collega \(p(i)\) alla transizione.
Scatto di una transizione
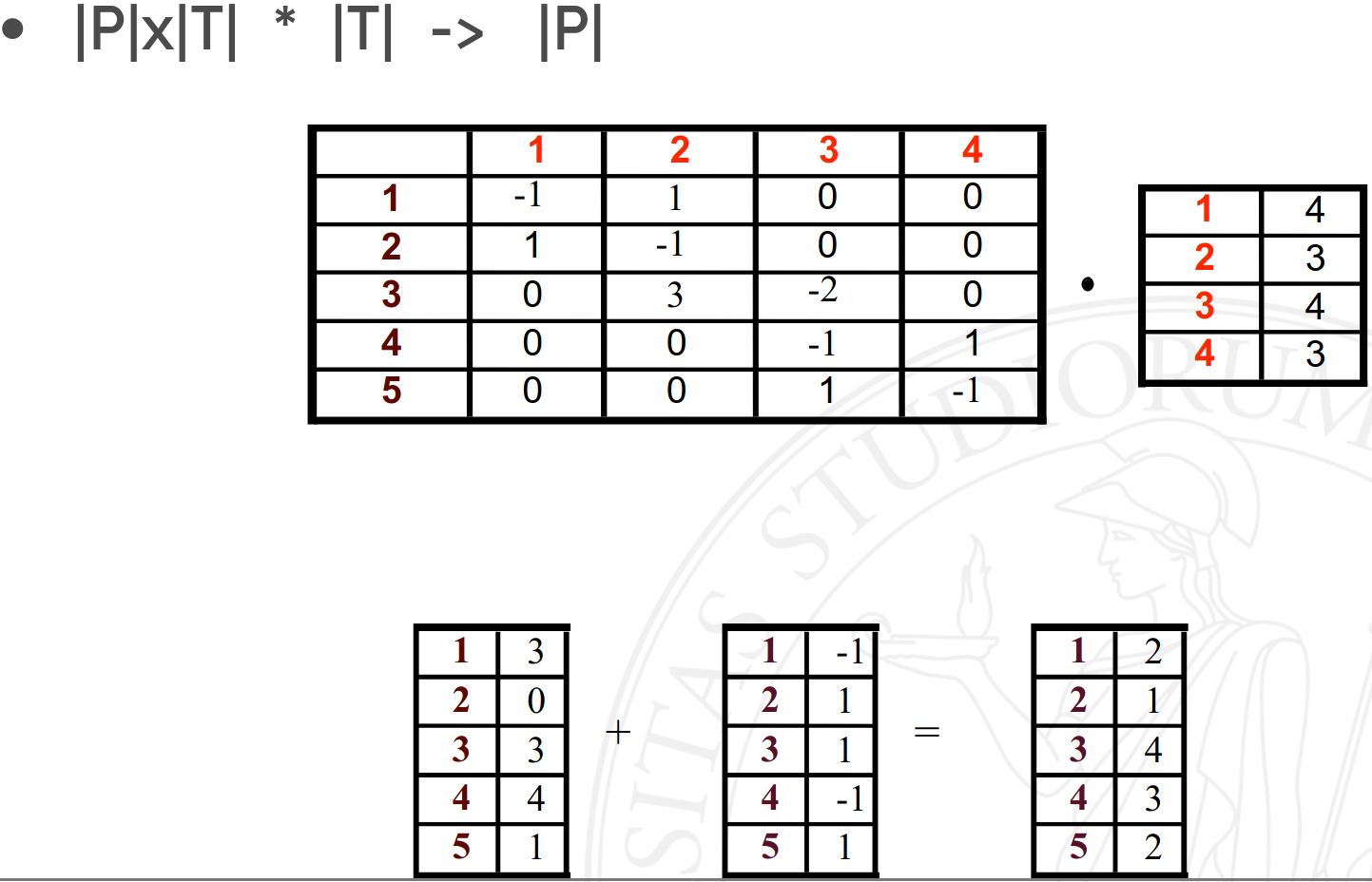
Lo scatto di una transizione \(j\) in una marcatura \(m\) produce una marcatura \(m’\) che si ricava sottraendo elemento per elemento al vettore di partenza la colonna \(j\)-esima della matrice di input e quindi sommando al risultato la colonna j-esima della matrice output.
$$ \boxed{\boxed{m [ \ t(j) >} \: m’} \Longleftrightarrow m’ = m - I[.][j] + O[.][j] \\ \textit{o se proprio vogliamo essere precisi…} \\ \boxed{\boxed{m [ \ t(j) >} \: m’} \Longleftrightarrow \forall i \in 1..\vert P \vert \quad m’[i] = m[i] - I[i][j] + O[i][j]. \\ $$
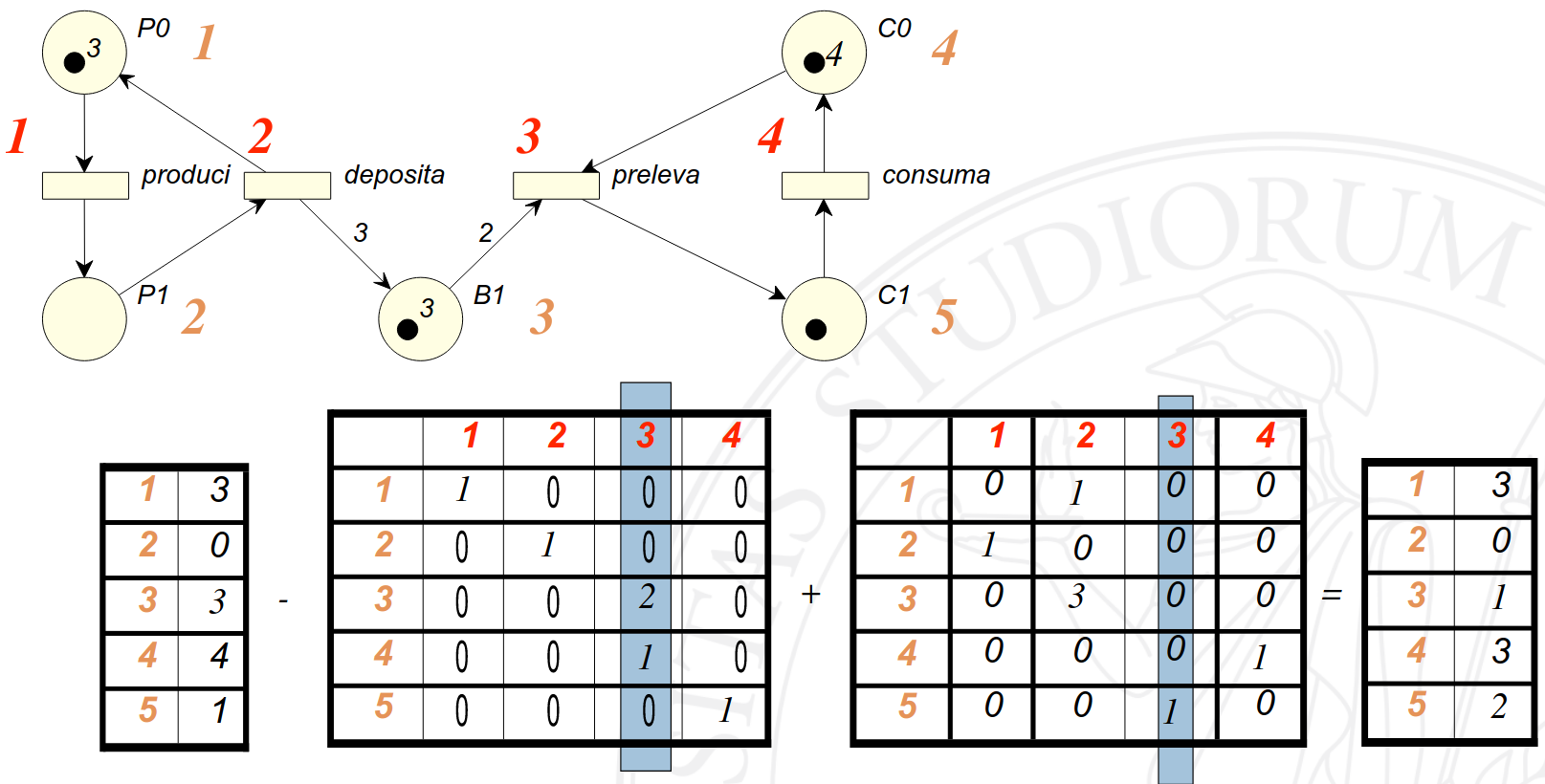
È importante notare come nell’operazione sopra due operandi su tre sono matrici costanti (\(I\) e \(O\)): è quindi possibile pre-calcolare \(O - I\) per efficienza.
Matrice di incidenza \(C\)
La matrice \(O - I\) presentata sopra è infatti chiamata matrice di incidenza e si indica con la lettera \(C\). È utile per ottimizzare l’operazione scatto di una rete in forma matriciale. In formule:
$$ \forall i \in 1..\vert P \vert, \, \forall j \in 1.. \vert T \vert \quad C[i][j] = O[i][j] - I[i][j]. $$
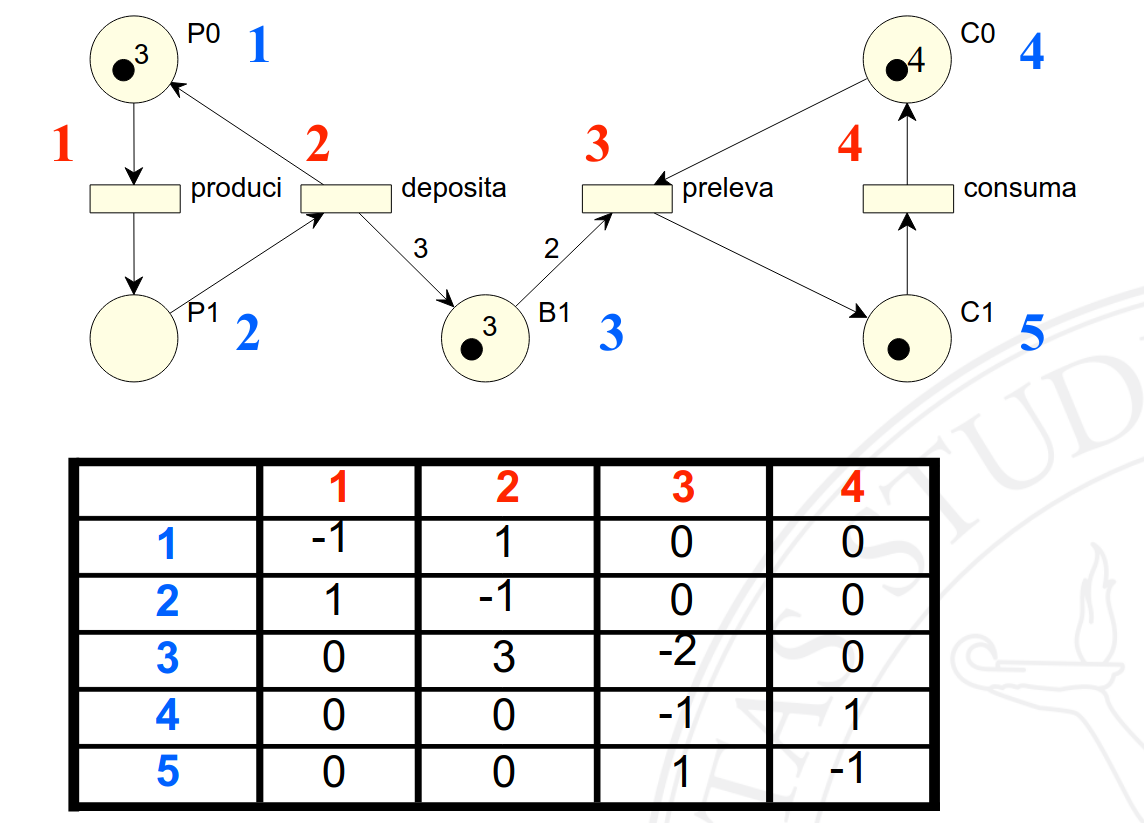
\(C\) non sostituisce le matrici di input \(I\) e output \(O\), in quanto \(I\) è ancora necessaria per calcolare l’abilitazione di una transizioni. Per le reti non pure, infatti, il valore presente in un qualsiasi posto della matrice potrebbe essere dato da una qualsiasi combinazione di pesi relativi ad archi in ingresso ed uscita, in quanto per la stessa posizione \(\langle i, \, j \rangle\) entrambe le matrici potrebbero assumere un valore.
Sequenze di scatti
Si consideri una sequenza di \(n\) scatti che porti la rete da una marcatura iniziale \(M\) a una marcatura \(M^n\).
Ripetendo il seguente processo per \(n\) scatti
$$ \boxed{\boxed{M [ \ t_1 >} \: M’ \vphantom{M’‘}}, \; \boxed{\boxed{M’ [ \ t_2 >} \: M’‘} \rightarrow \boxed{\boxed{M [ \ t_1t_2 >} \: M’’}, $$
si rinomini la sequenza ottenuta nel seguente modo:
$$ \boxed{\boxed{M [ \ s >} \: M^{(n)}}. $$
Esiste un legame diretto tra la marcatura iniziale e quella finale, che non preveda eseguire i singoli passi? A livello di matrici, l’esecuzione in sequenza di \(x_1\) volte di \(t_1\), \(x_2\) volte di \(t_2\) fino a \(x_n\) volte di \(t_n\) è fattorizzabile. Definendo un vettore \(s\) tale per cui
$$ \forall j \in 1..\vert T \vert \quad s[j] = \text{# di volte in cui $t(j)$ scatta} $$
è facile notare come l’ordine di scatto non conta. Calcolando quindi \(Cs\) è quindi possibile calcolare l’effetto netto dell’intera sequenza di scatti, svolgendo un’unica operazione. Sommando \(Cs\) alla marcatura iniziare \(M\), si ottiene lo stato della marcatura finale \(M^{(n)}\).
$$ M^{(n)} = M + C s. $$
È opportuno specificare che \(s\) non è in grado di determinare l’esistenza o l’ordine della sequenza presa in considerazione. Non è quindi possibile sapere se \(s\) corrisponde a una sequenza ammissibile di scatti, ma è facile escluderlo: se \(M^{(n)}\) contiene numeri negativi, allora \(s\) corrisponde sicuramente ad una sequenza inammissibile. In generale, se anche in un solo passo intermedio \(M^{(i)}\) è negativo, allora la sequenza considerata non è ammissibile.
In conclusione, è possibile effettuare questo calcolo solo se si è certi che la sequenza di scatti sia ammissibile.
Di seguito è presente un esempio che potrebbe chiarire le idee.