Eliminazione pesi sugli archi
In precedenza è stato accennato che per ogni rete avente dei pesi sugli archi è possibile crearne una equivalente senza pesi sugli archi (ovvero avente tutti gli archi di peso 1).
Per fare ciò è necessario considerare due casi distinti, ovvero quello con peso sugli archi in ingresso ad una transizione e quello con peso sugli archi in uscita ad una traniszione.
Pesi su archi in ingresso
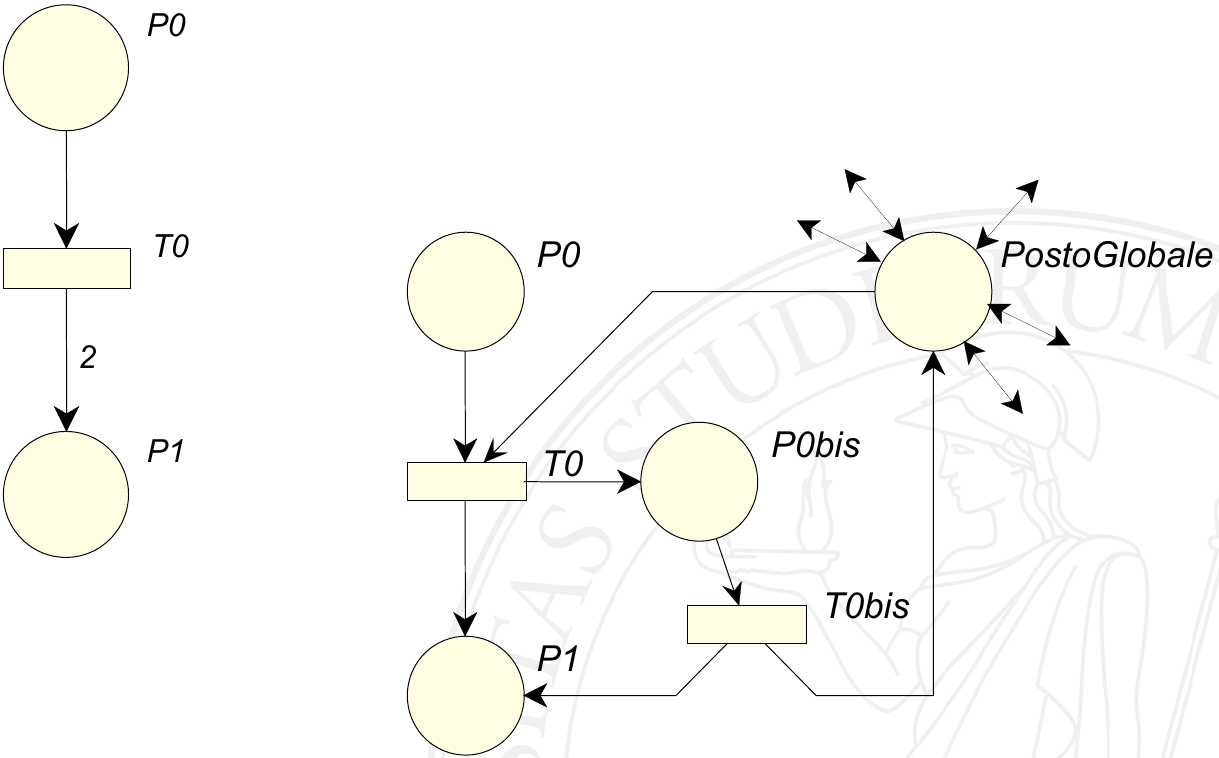
Per poter effettuare questa modifica è necessario avere lo scatto di una nuova transizione (in quanto ovviamente non è possibile collegare due archi dallo stesso posto alla stessa transizione), ma non basta. Dopo lo scatto di \(t_0\) è infatti possibile che \(t_0^\text{BIS}\) non scatti e la rete evolva senza che in \(p_1\) ci sia il giusto numero di gettoni (problema di concorrenza).
Per risolvere questo problema si sfrutta una sorta di lock, ovvero un posto collegato bidirezionalmente con tutte le transizioni della rete tranne per \(t_0\), a cui è collegato solo in ingresso, e per \(t_0^\text{BIS}\), a cui è collegato solo in uscita. In questo modo è come se lo scatto di \(t_0\) sia scomposto logicamente in due parti: quando \(t_0\) scatta viene attivato il lock in modo tale che nessun’altra transizione sia abilitata e, successivamente, lo scatto di \(t_0^\text{BIS}\) lo rilascia. Questo ovviamente non obbliga \(t_0^\text{BIS}\) a scattare immediatamente, però è certo che la rete non potrà evolvere in alcun altro modo e quindi non si creeranno marcature non esistenti nella rete originale. Questa soluzione non è molto elegante perchè esiste un posto avente in ingresso un arco per ogni transizione della rete.
Pesi su archi in uscita
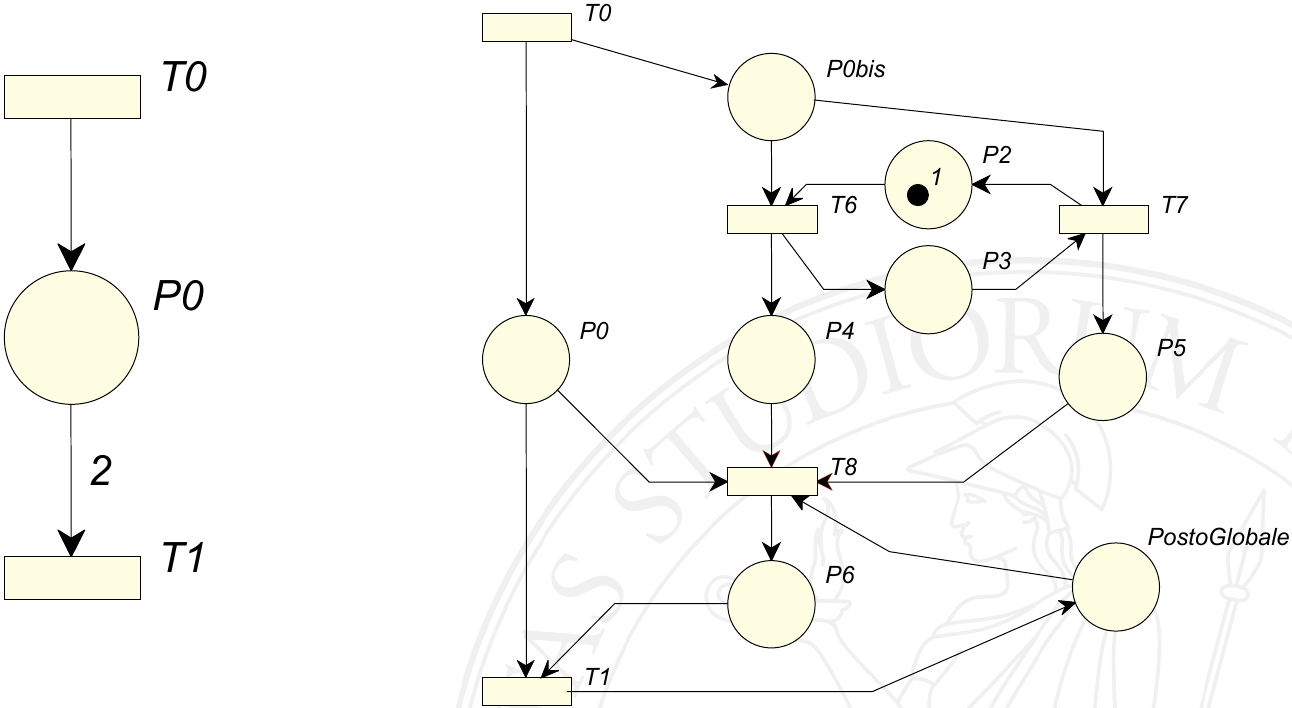
In questo caso il peso da rimuovere è su un arco che esce da un posto ed entra in una transizione, quindi è necessario che vengano distrutti due gettoni dallo stesso scatto.
L’approccio da utilizzare è simile: è infatti presente un posto globale che fa da lock in modo da risolvere il problema di concorrenza tra \(t_8\) e \(t_1\).
In questo caso però è presente un ulteriore problema, ovvero al momento dello scatto di \(t_8\) il gettone in \(p_0\) viene consumato, di conseguenza \(t_1\) non può scattare. Inoltre il resto della rete rimane bloccata, in quanto all’interno del posto globale non è più presente il gettone che è stato consumato sempre dallo scatto di \(t_8\).
Questo deadlock può essere risolto aggiungendo un controllo sul posto \(p_0\), in modo tale che possa scattare solo quando possiede due o più gettoni: in questo modo non può verificarsi la situazione in cui \(t_8\) scatti senza un successivo scatto di \(t_1\).
Il meccanismo della rete inizia ad essere molto complesso; nell’esempio viene mostrato solo il caso in cui devono essere consumati due gettoni. In altri casi con più gettoni, o con situazioni differenti, la rete aumenterebbe ulteriormente di complessità. Risulta quindi più facile pensare la rete in modo differente.
La tenica descritta sopra non è infatti l’unica esistente per modellare il sistema: nonostante possa essere adatta per questo particolare esempio, è comunque possibile trovarne un’altra per modellare una rete senza fruttare i pesi o una loro traduzione meccanica.
Reti \(\mathcal{C/E}\)
Le reti \(\mathcal{C/E}\) (condizioni eventi) sono delle particolari reti più semplici, in cui tutti gli archi hanno peso uno e tutti i posti hanno capacità massima uno.
A prima vista, questo tipo di rete può risultare poco modellabile, ma è in realtà più semplice ed immediata da capire: infatti i posti rappresentano delle condizioni che possono essere vere o false ed in base ad esse è possibile il verificarsi di certi eventi, rappresentati dalle transizioni.
Ogni rete \(\pt\) limitata è traducibile in un’equivalente rete \(\mathcal{C/E}\).
Per le reti illimitate non è invece possibile trovare una traduzione, siccome non si possono rappresentare infiniti stati con un tipo di rete che per definizione è limitata.