Albero di raggiungibilità

Per generare l’albero di raggiungibilità di una rete di Petri si può applicare il seguente algoritmo.

1. crea la radice dell’albero corrispondente alla marcatura iniziale \(M_0\) ed etichettala come nuova;

2. finché esistono nodi etichettati come “nuovi” esegui:

   1. seleziona una marcatura \(M\) etichettata come “nuova”;
      prendila in considerazione e rimuovi l’etichetta “nuova”.

   2. se la marcatura \(M\) è identica ad una marcatura di un altro nodo allora:

      • etichetta \(M\) come “duplicata”;
      • continua passando alla prossima iterazione.

   3. se nella marcatura \(M\) non è abilitata nessuna transizione allora:

      • etichetta \(M\) come “finale”;

      • situazione di deadlock.

      altrimenti esegui:

      • finché esistono transizioni abilitate in \(M\) esegui:

        • per ogni transizione \(t\) abilitata in \(M\) esegui:

          1. crea la marcatura \(M’\) prodotta dallo scatto di \(t\);

          2. crea un nuovo nodo corrispondente alla marcatura \(M’\);

          3. aggiungi un arco nell’albero al nodo corrispondente di \(M\) al nodo di \(M’\);

          4. etichetta la marcatura \(M’\) come “nuova”.

Esempio

Di seguito è mostrata una consegna di un esercizio riguardo gli alberi di raggiungibilità.

Modellare tramite una rete di Petri l’accesso ad una risorsa condivisa tra quattro lettori e due scrittori, ricordandosi che i lettori possono accedere contemporaneamente, mentre gli scrittori necessitano di un accesso esclusivo.

Come primo approccio, si possono creare due reti, una per i lettori e una per gli scrittori. È possibile successivamente procedere modellando la Risorsa condivisa collegando le diverse parti create.

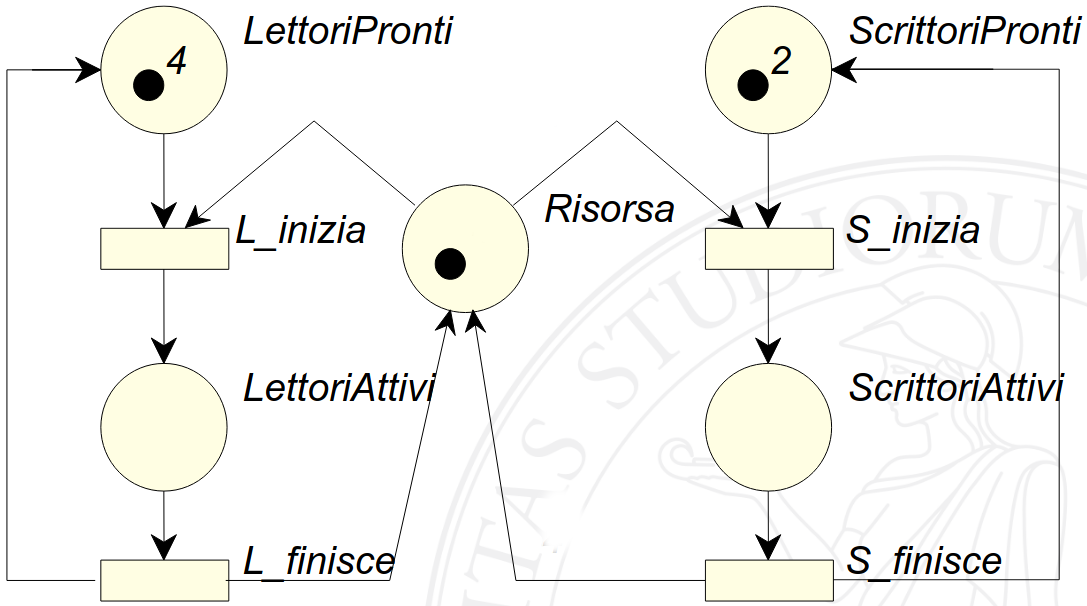
Essendo presente un solo gettone nel posto Risorsa, i lettori non sono in grado di accedervi contemporaneamente. Per risolvere questo problema, si può aumentare il numero di gettoni all’interno di Risorsa a 4. Per evitare che gli scrittori possano accedere alla Risorsa mentre viene letta, è possibile aggiungere un peso pari a 4 sugli archi da “Risorsa” a “S_inizia” e da “S_finisce” a “Risorsa”.

Così facendo, per accedere alla Risorsa uno scrittore dovrà attendere che tutti i token saranno depositati in essa, garantendo che nessun’altro sta utilizzando la risorsa.

Il risultato finale è il seguente.

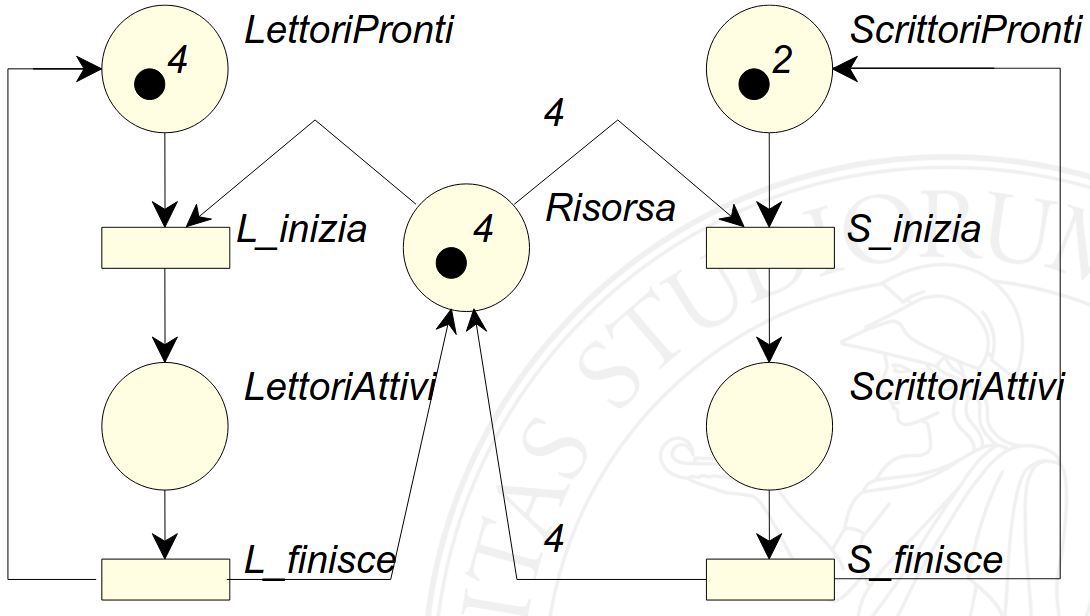
Costruzione dell’albero di raggiungibilità

Una volta creata la rete finale, è possibile generare l’albero di raggiungibilità seguendo l’algoritmo precedente.

Il primo passo è creare il nodo radice corrispondente alla marcatura iniziale e marcarlo come nuovo: \(\nodenew{40420}\).

Successivamente, occorre procedere per ogni nodo marcato come nuovo. In questo caso l’unico nodo marcato come nuovo è \(\nodenew{40420}\). Dopo aver rimosso l’etichetta nuovo si verifica che, partendo dalla radice dell’albero, non siano già presenti altri nodi uguali. Essendo \(\node{40420}\) esso stesso la radice (e unico nodo dell’albero), si procede.

A questo punto, per ogni transizione abilitata nella marcatura presa in considerazione (\(\node{40420}\)) la si fa scattare generando le altre marcature marcate come nuovo (\(\nodenew{40011}\) e \(\nodenew{31320}\)) che quindi si collegano con un arco alla marcatura originale (\(\node{40420}\)).

La situazione attuale è la seguente.

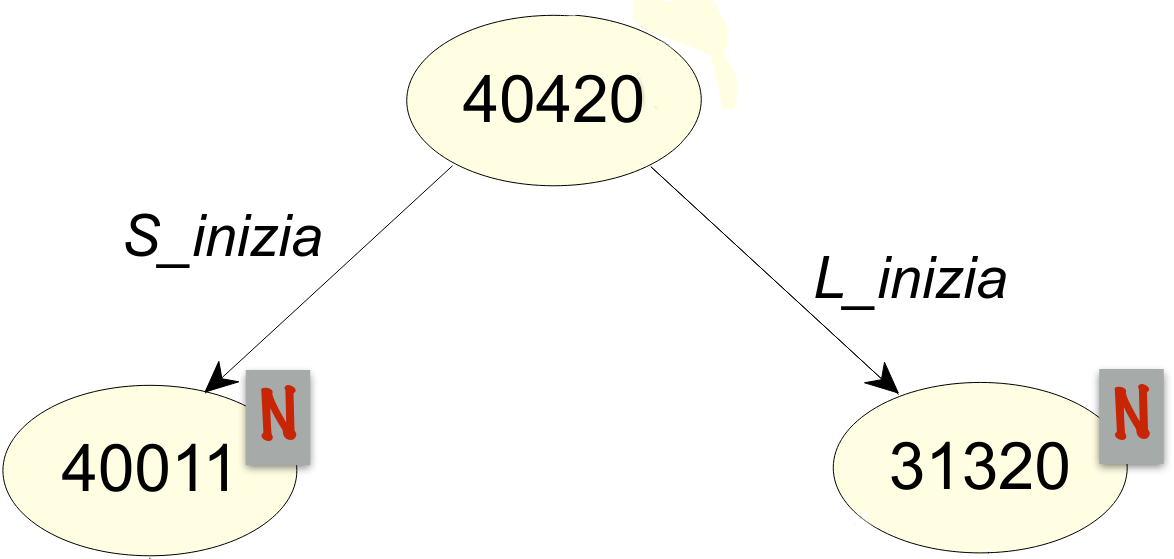
Si procede quindi con l’algoritmo ripetendo i passi fino ad arrivare in una situazione in cui non esistono più nodi nuovi, marcando nel mentre come duplicati tutti i nodi che si re-incontrano nonostante siano già presenti almeno una volta nell’albero.

La situazione finale sarà la seguente.

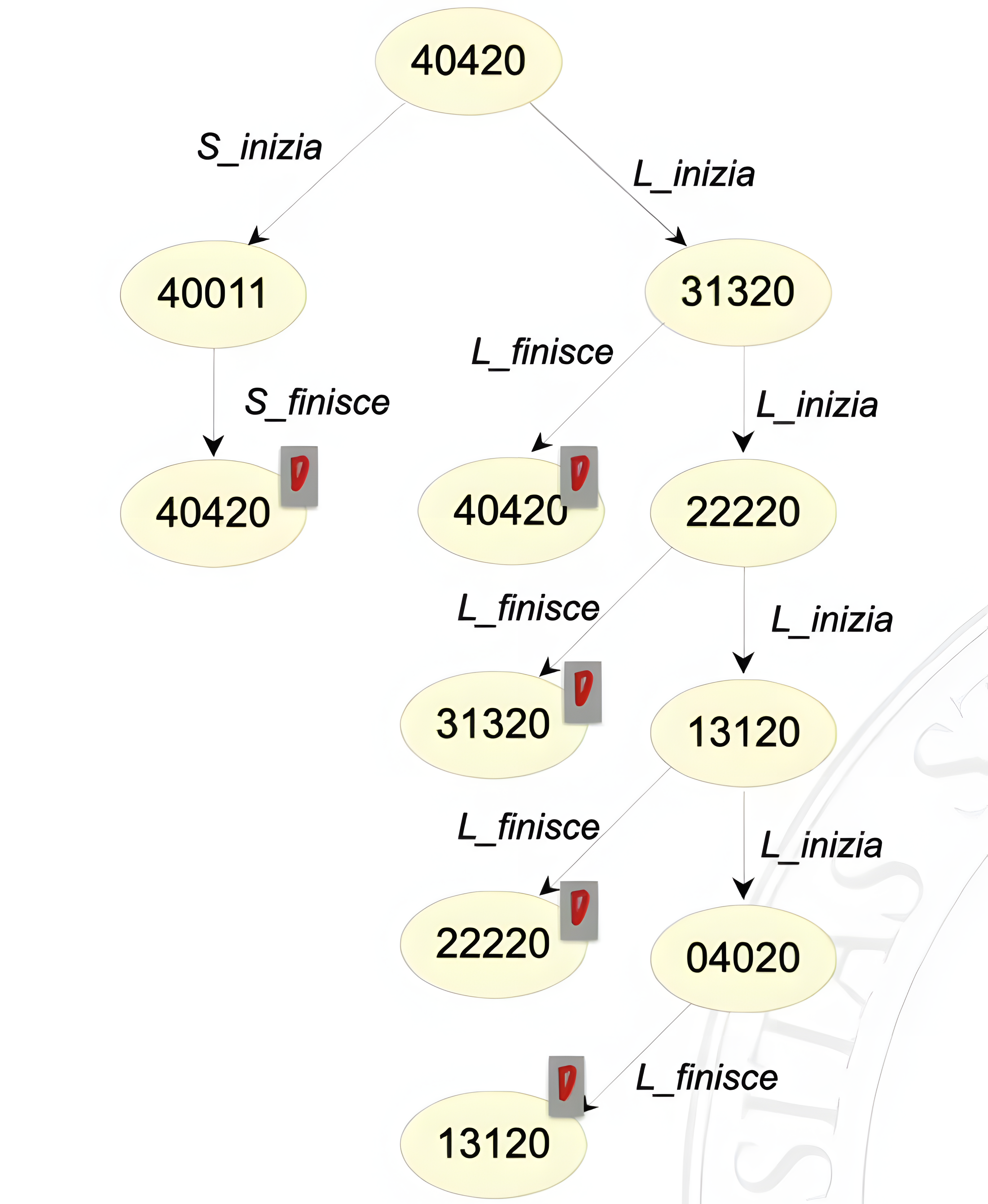
L’albero di raggiungibilità sopra in figura è a ora completo e rappresenta tutti gli stati raggiungibili.

Grazie a questo albero, se si volesse verificare che gli scrittori sono in mutua esclusione con i lettori, basterà controllare se esiste una marcatura in cui il secondo e il quinto numero (rispettivamente “LettoriAttivi” e “ScrittoriAttivi”) sono entrambi contemporaneamente maggiori di zero. Si può verificare in modo esaustivo (model checking) guardando tutti i nodi dell’albero. Inoltre si può verificare se gli scrittori si escludono a vicenda, controllando se in ogni marcatura l’ultimo numero (“ScrittoriAttivi”) è maggiore di uno. Si infine verificare l’assenza di deadlock, data dalla presenza o meno di nodi terminali.

Collassando i nodi aventi la stessa marcatura, si può verificare dall’albero di raggiungibilità se la rete è viva.

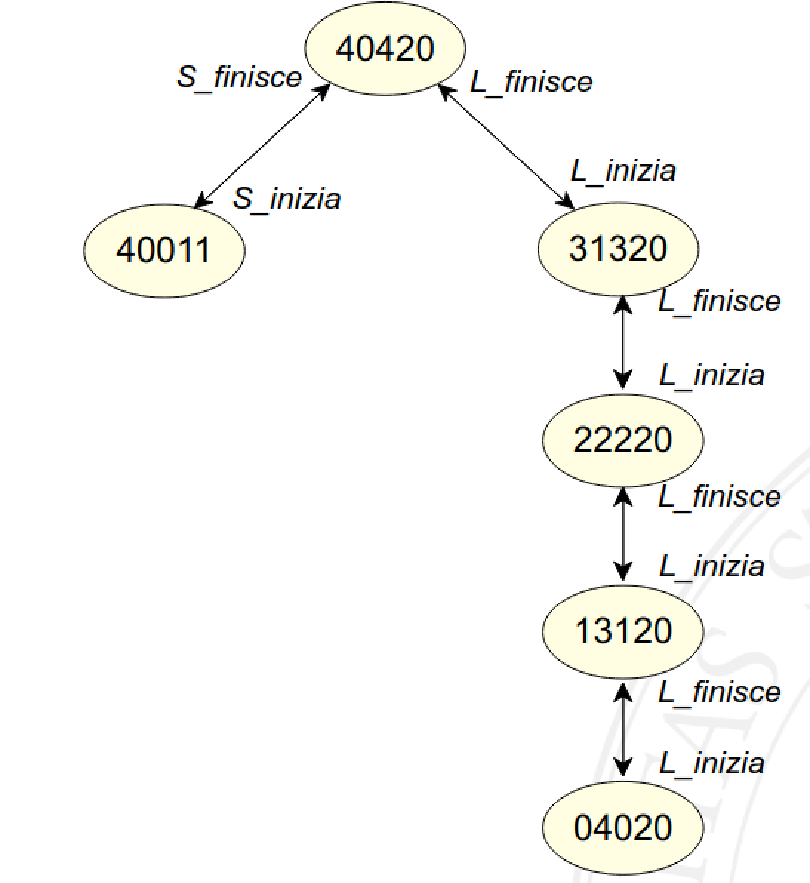
La rete è anche reversibile in quanto ogni stato è uno stato base ed è quindi possibile raggiungere da ogni stato tutti gli altri stati.
Avendo questo grafo è quindi facile capire che la rete è viva, in quanto sono rappresentate tutte le transizioni all’interno del grafo, e siccome il sistema è reversibile è sempre possibile riportarsi ad una situazione in cui si può far scattare una transizione.

Limiti

• Per poter creare un albero di raggiungibilità è necessario enumerare tutte le possibili marcature raggiungibili, di conseguenza la rete deve essere obbligatoriamente limitata: non sarebbe altrimenti possibile elencare tutti i nodi.
• la crescita (esponenziale) del numero degli stati globali può risultare velocemente ingestibile per una rete limitata.

Inoltre:

• Questa tecnica di analisi non è in grado di rilevare se una rete è limitata o meno;
• Nel caso in cui si sappia già che la rete è limitata:
  • l’albero di raggiungibilità non perde informazioni ed è la esplicitazione degli stati della rete (quindi ne è di fatto la FSM corrispondente).