Macchine a stati finiti

È meccanicamente possibile trasformare una macchina a stati finiti in una rete di Petri.

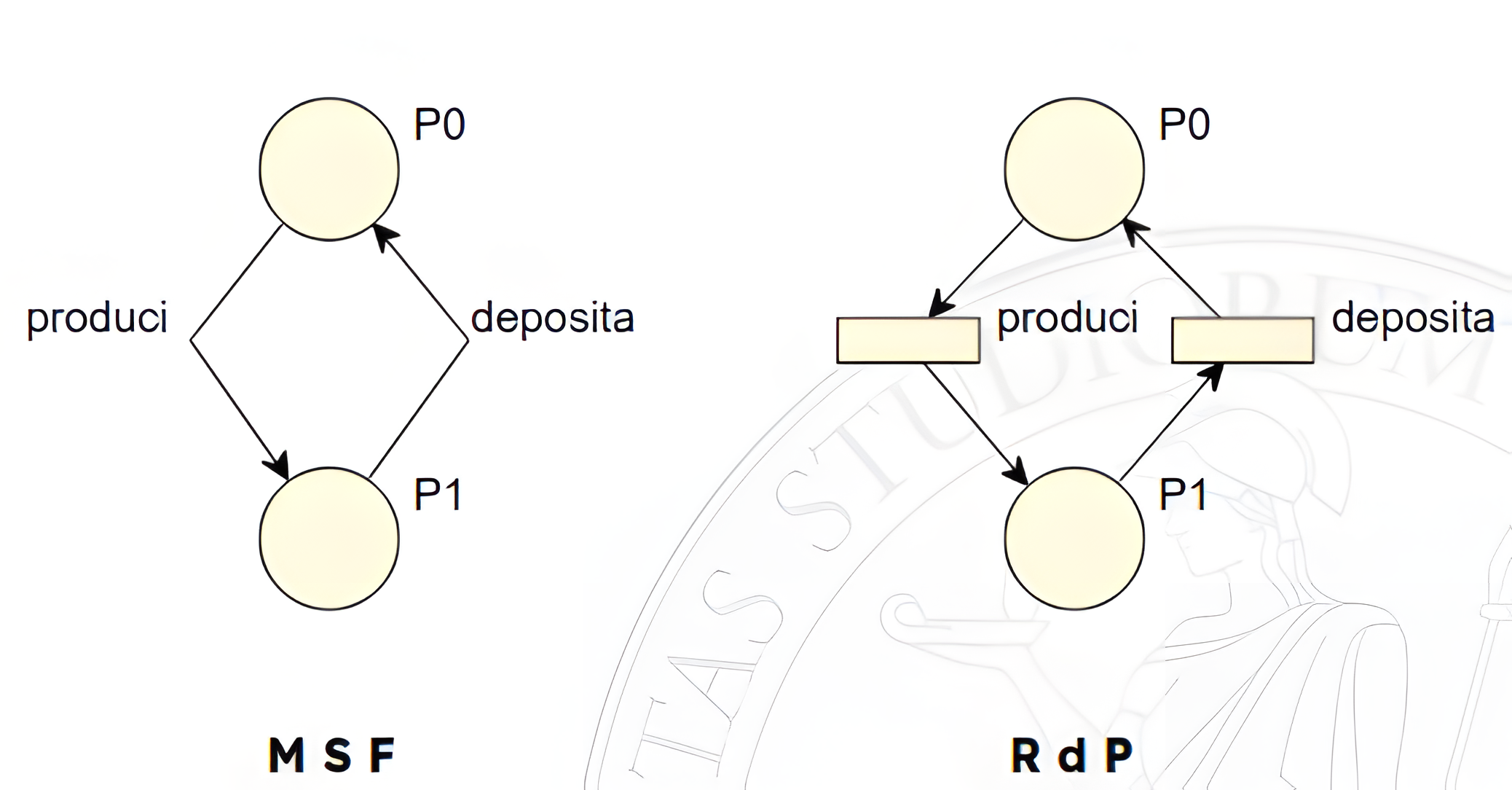
Riferendosi all’esempio del produttore, l’unico problema è l’esistenza di collegamenti diretti tra posti: come è stato detto in precedenza questo non è possibile in una rete di Petri. Sarà quindi necessario interporre tra i posti delle transizioni per avere una rete di Petri valida.
Immaginando di mettere un solo gettone in uno dei due posti della rete appena creata, questo indicherà lo stato attivo presente nella macchina a stati finiti.
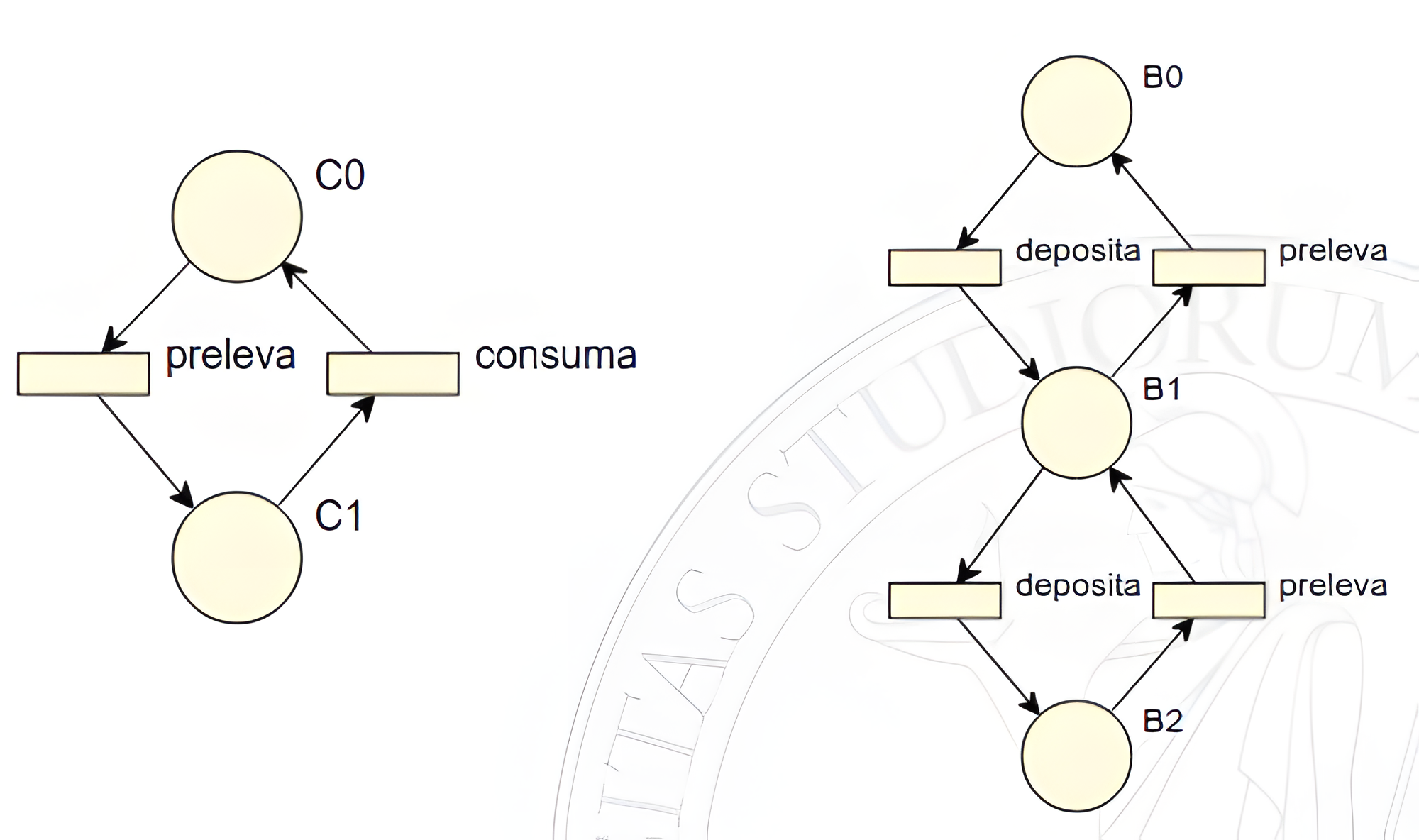
Seguendo questi passaggi diventa banale mappare una macchina a stati finiti su una rete di Petri: di seguito è possibile osservare l’operazione analoga eseguita sulle FSM di un consumatore e di un buffer.

Componendo le reti di Petri di produttore, consumatore e buffer appena create, si crea la seguente.

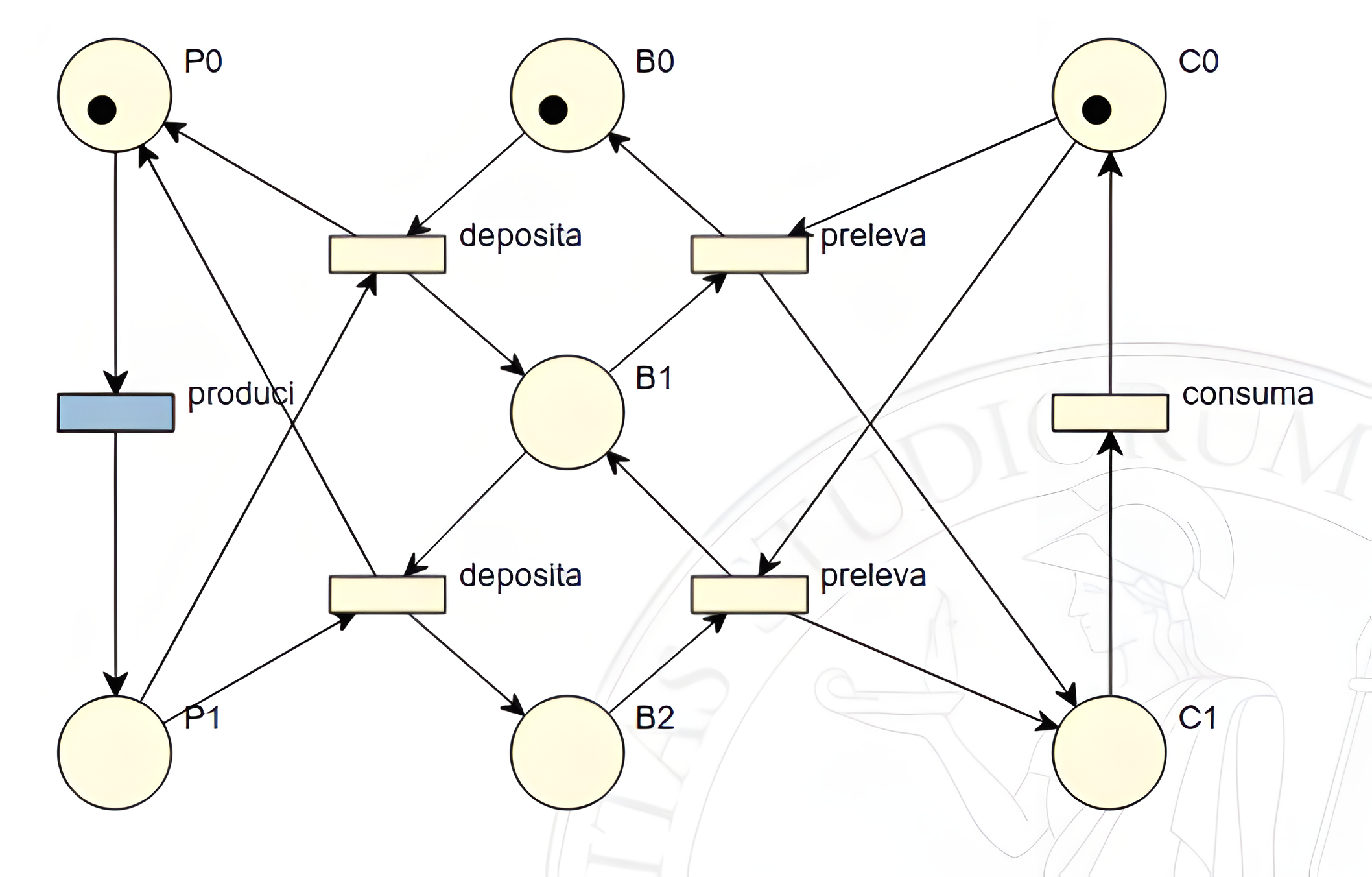
In termini di automi a stati finiti, per trovare gli stati raggiungibili da questa composizione sarebbe stato necessario eseguire il prodotto cartesiano tra gli stati delle tre macchine a stati finiti combinate tra loro. Trattandosi invece di una rete di Petri, è sufficiente unire tutti gli identificatori uguali in un unico identificatore (ad esempio la transizione deposita della rete produttore e della rete buffer) e aggiungere a quest’ultimo tutti collegamenti posseduti dagli identificatori uniti.

ATTENZIONE: nell’esempio della rete composta le coppie di transizioni “preleva” e “deposita” dovrebbero avere due nomi differenti, ma siccome sono indicate con due rettangoli diversi è stato omesso questo particolare. In termini matematici devono avere nomi differenti.

Precedentemente è stato detto che, nel caso di una rappresentazione di una FSM in termini di una rete di Petri, si rappresenta lo stato attivo nella FSM con un gettone: di conseguenza, portando all’interno della rete composta tutti i gettoni delle varie reti si arriva ad ottenere il risultato descritto dall’immagine precedente, in cui tutte le “entità” (consumatore, produttore e buffer) mantengono la propria individualità (è infatti presente un gettone per ogni entità).

In questo caso si può quindi notare che il produttore è pronto a produrre, il buffer è vuoto e il consumatore è pronto a consumare una volta che il buffer avrà al suo interno qualcosa.

Come evolve questa rete?

Per rispondere a questa domanda la prima cosa da considerare è quali sono le transizioni abilitate: in questo caso si tratta solo della transizione produci sotto a \(p_0\), in quanto è l’unica ad avere tutti gli elementi del suo preset con un numero di gettoni sufficienti a farla scattare; \(p_0\) possiede infatti un gettone e l’arco ha peso 1 (quando non è specificato il peso è 1).
Una rete di Petri non forza lo scatto di alcuna transizione, quindi volendo si potrebbe rimanere nello stato corrente all’infinito senza far mai scattare produci. Se però produci scatta, il gettone in \(p_0\) viene distrutto e in \(p_1\) viene generato un nuovo gettone.

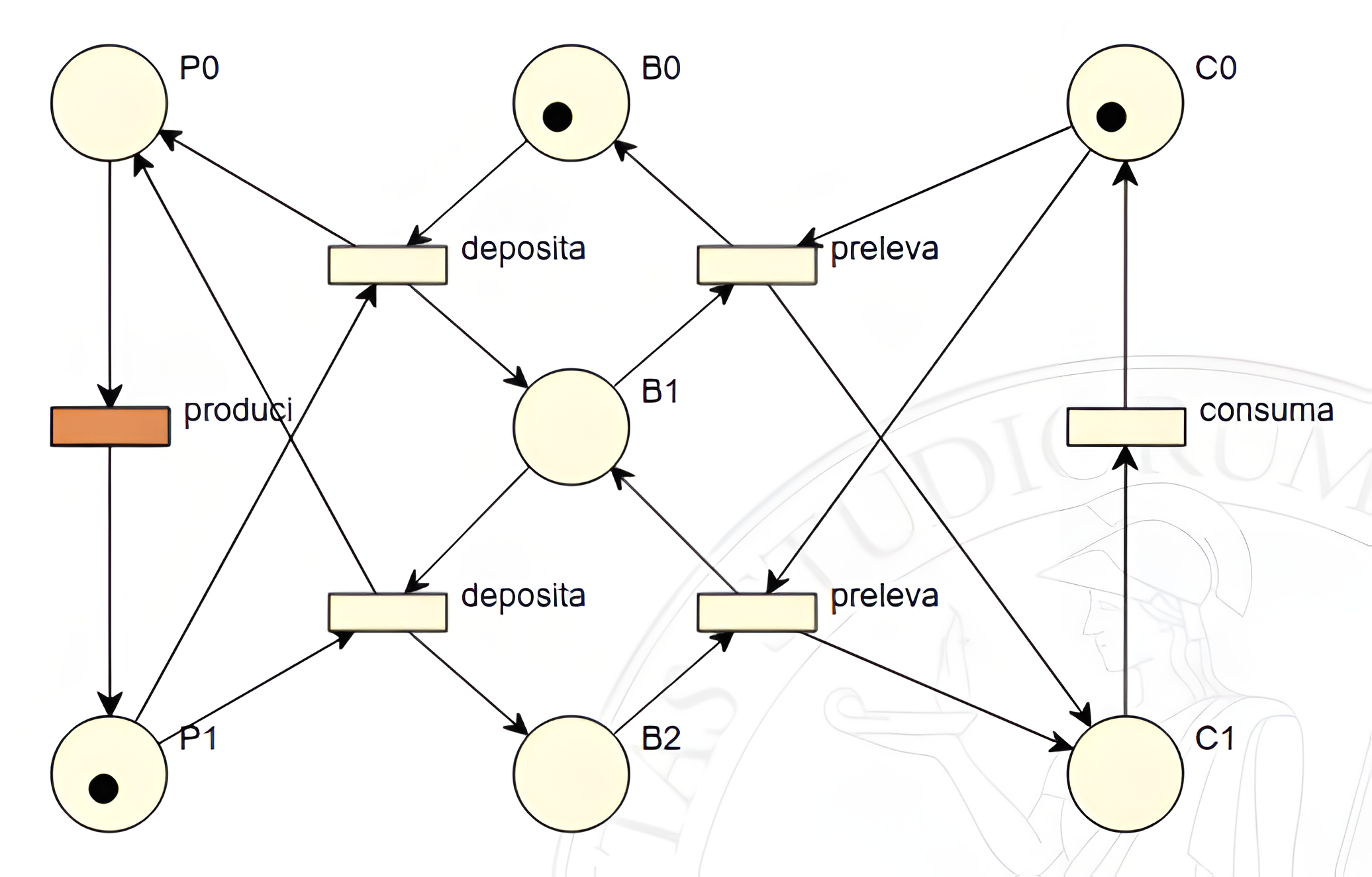
Dopo questo scatto la rete di Petri si trova in una situazione in cui il produttore ha prodotto qualcosa ed è pronto a depositarlo nel buffer: a questo punto non resta che porsi nuovamente la domanda “quali transizioni sono abilitate?” per capire come può procedere l’evoluzione della rete.
È facile notare come la transizione deposita sotto \(b_0\) sia l’unica abilitata e di conseguenza, se dovesse scattare, il risultato sarebbe il seguente:

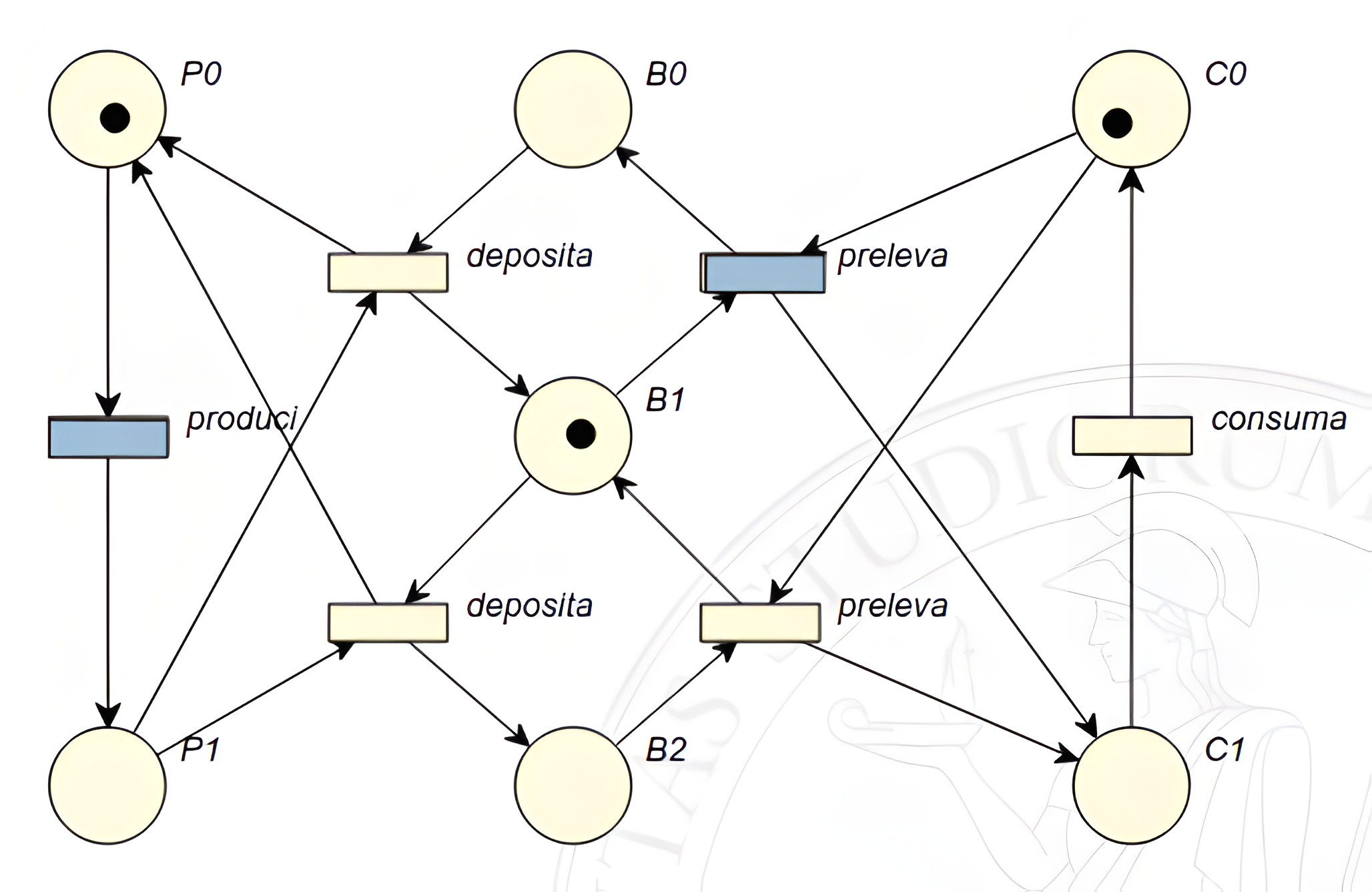
Ora è possibile identificare una situazione particolare, ovvero quella in cui le transizioni pronte a scattare sono due. Sorge spontanea la domanda: “quale delle due transizioni scatta prima?”. Nelle reti di Petri descritte fino ad ora non è stato presentato lo scatto simultaneo delle transizioni, ma nulla vieta che possa avvenire in un contesto reale. In tal caso si tratterebbe di un’istanza di non determinismo, ovvero non si può dire quale transizione deve scattare. Sono quindi 3 le situazioni che si possono verificare:

• scatta la prima transizione;
• scatta la seconda transizione;
• non scatta nessuna transizione (la non evoluzione è comunque un’evoluzione).

Nel caso in cui fosse stato necessario definire che una delle due transizioni scatti prima dell’altra, ci si troverebbe di fronte ad una rete non corretta: è infatti possibile modificare la rete in modo tale che imponga un ordine di scatto alle transizioni.

Sfruttare le reti di Petri

A questo punto è possibile chiedersi se si stiano sfruttando realmente tutte le potenzialità delle reti di Petri, siccome la rete dell’esempio precedente è stata ricavata da un automa a stati finiti. Per capire ciò è possibile osservare un secondo esempio in cui è presentata una rete alternativa alla precedente, ma con lo stesso scopo.

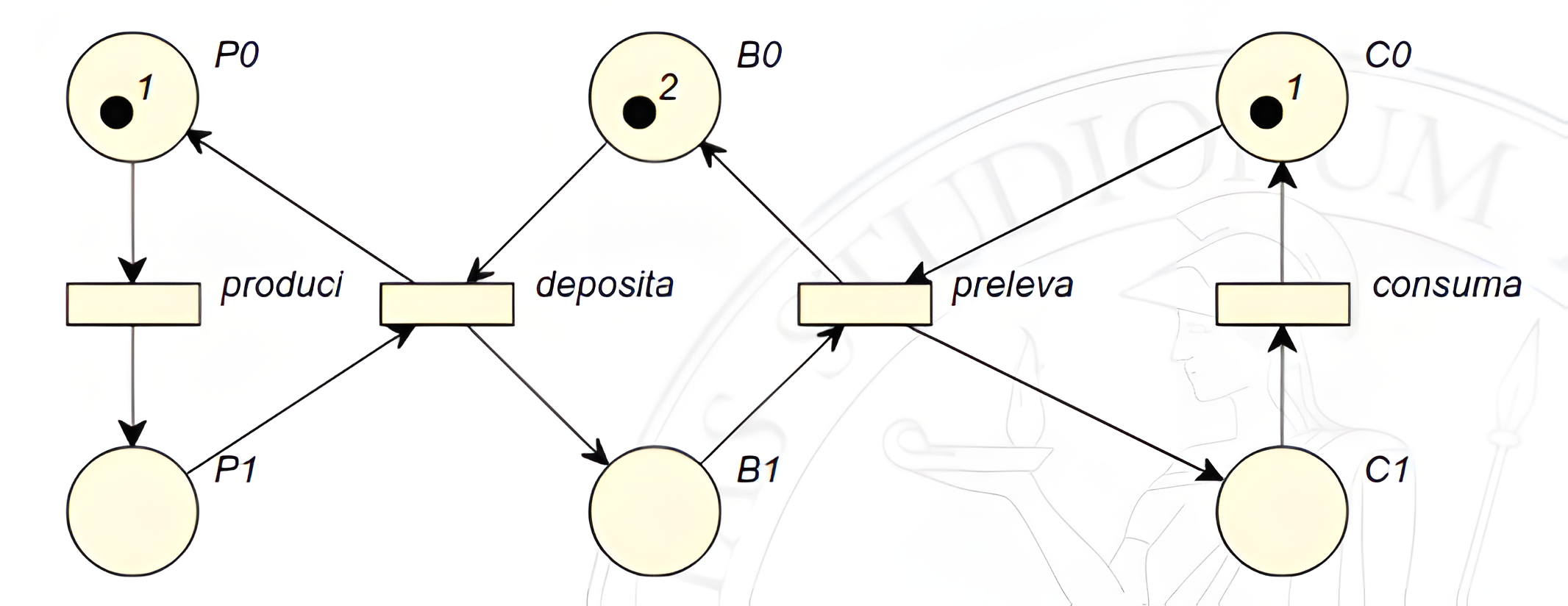
La differenza che salta subito all’occhio è il numero di gettoni presenti all’interno di \(b_0\) che indicano il numero di posizioni libere nel buffer. Questo è un vantaggio perchè se il buffer dovesse cambiare la sua capienza, sfruttando questa rete è sufficiente modificare la marcatura di \(b_0\) e il problema sarebbe risolto; la rete precedente avrebbe invece bisogno di una pesante modifica per essere adattata.
Di conseguenza si può applicare lo stesso concetto per il consumatore e per il produttore: aumentandone il numero dei gettoni (rispettivamente in \(p_0\) e \(c_0\)) aumenterebbe il numero di entità in grado di produrre e consumare.

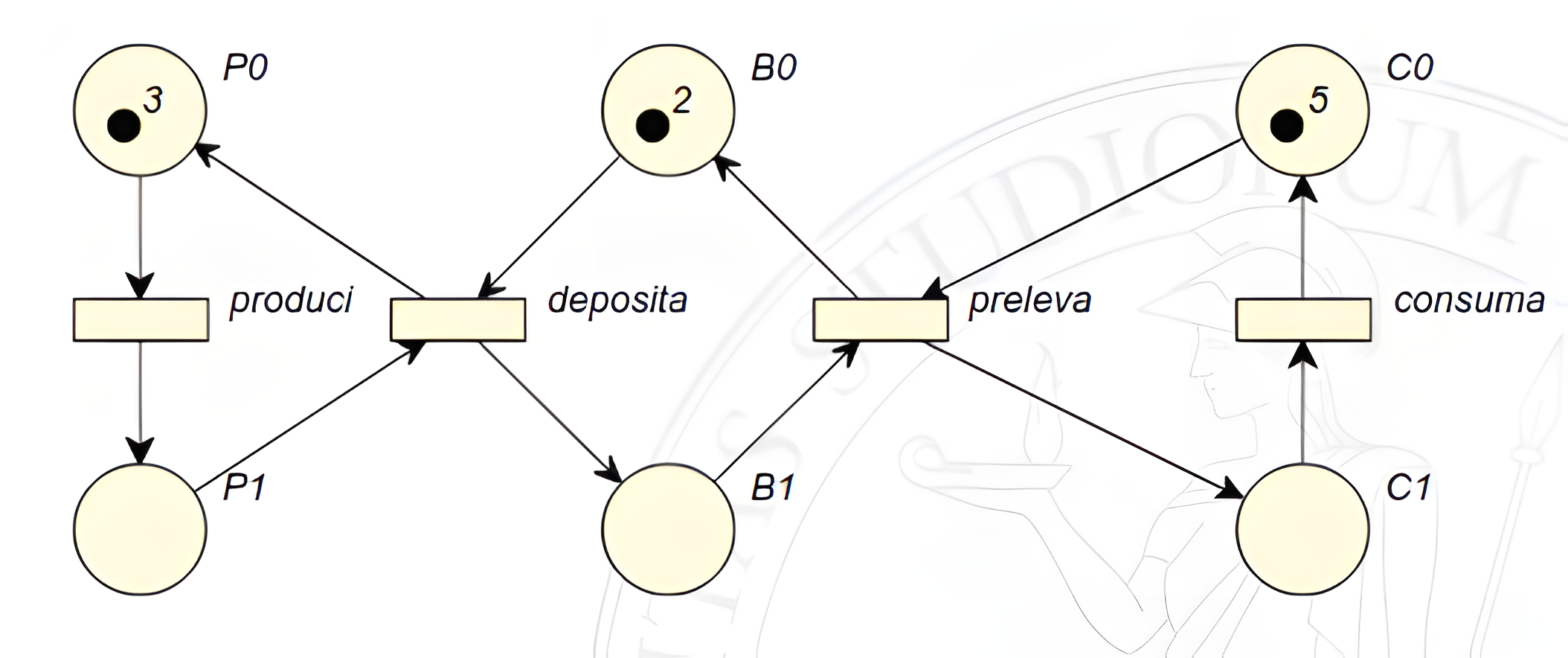
È possibile affermare quindi che cambiando il numero di gettoni è possibile moltiplicare gli elementi del sistema di cui si vuole tracciare l’evoluzione. Si sottolinea ancora che questo risulterebbe molto oneroso in termini di dimensioni se fosse stato riadattato in una macchina a stati finiti.

Per definizione le macchine a stati finiti non possono rappresentare situazioni infinite, se si volesse quindi modificare ulteriormente l’esempio appena visto imponendo una capienza illimitata al buffer, non sarebbe possibile utilizzando una macchina a stati finiti. Sfruttando le reti di Petri invece è sufficiente eliminare l’identificatore del posto \(b_0\): in questo modo abbiamo una situazione in cui i produttori possono depositare senza limiti all’interno del buffer, mentre i consumatori non possono prelevare più elementi di quelli presenti nel buffer. Questo vincolo è imposto dalla marcatura di \(b_1\), infatti la transizione “preleva” può scattare al massimo \(n\) volte consecutivamente, dove \(n\) è la marcatura di \(b_1\) — assumendo che nel mentre non avvengano depositi da parte dei produttori.

Un altra modifica applicabile all’esempio sfrutta i pesi degli archi: ponendo un peso di 3 all’arco che collega deposita a \(b_1\) si può dire che il produttore crea e deposita tre prodotti, occupando tre posizioni nel buffer. Ponendo invece un peso di 2 all’arco che collega \(b_1\) a preleva si specifica che è possibile prelevare dal buffer due elementi alla volta. Questo esempio, in parte forzato, è utile per chiarire il fatto che nelle reti di Petri gli archi non sono semplici collegamenti, ma è possibile attribuirgli un significato.

Vengono infatti informalmente chiamati archi, rifacendosi alla terminologia dei grafi, ma in realtà indicano una relazione più profonda che coinvolge due identificatori: in questo esempio esiste infatti una relazione per cui ogni elemento prodotto occupa tre posizioni all’interno del buffer e un’altra relazione in cui ogni consumatore può prelevare obbligatoriamente due elementi alla volta. Tramite il peso degli archi è possibile creare delle situazioni ambigue: ad esempio se la relazione che coinvolge deposita e \(p_0\) avesse un peso di 2, ogni volta che viene prodotto qualcosa i produttori si moltiplicherebbero e ovviamente questa situazione indicherebbe che la rete è sbagliata, quindi è necessario fare attenzione ad evitare questo tipo di situazioni.

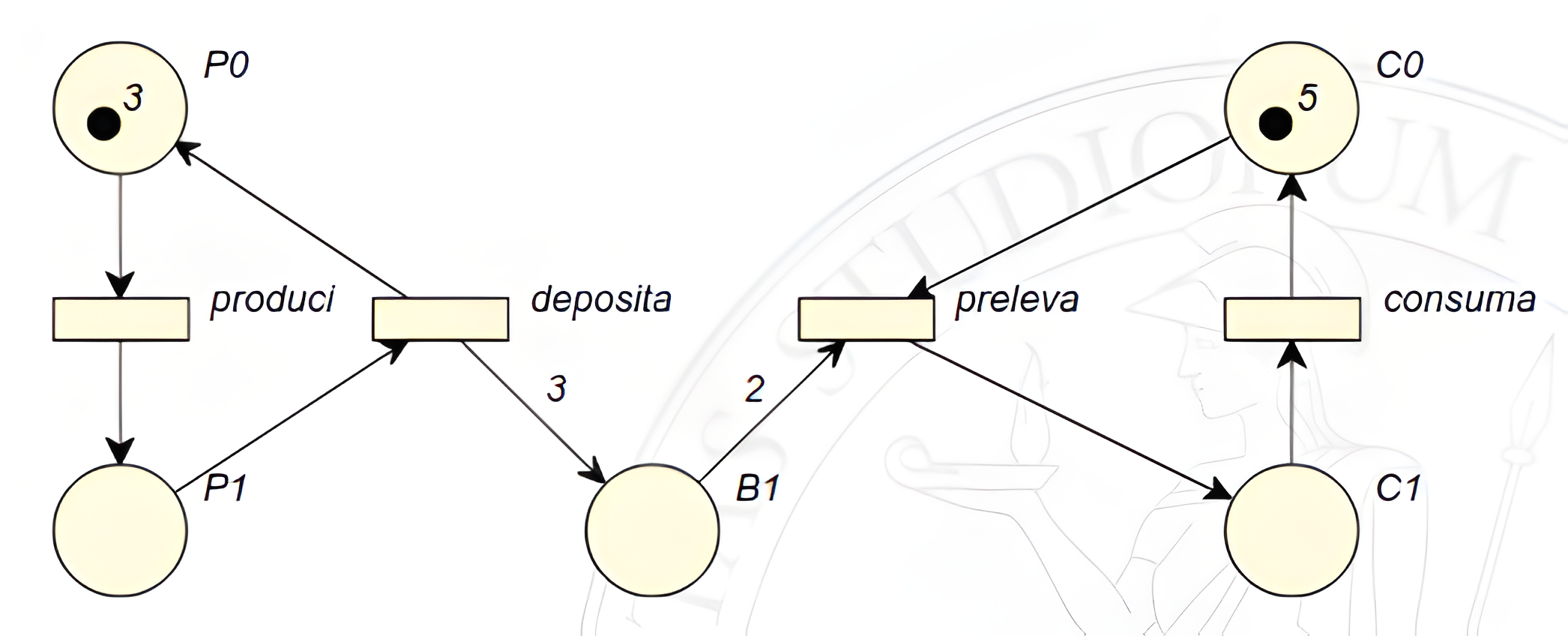
È da sottolineare che è possibile ridurre una rete P/T avente pesi sugli archi in una rete P/T senza pesi sugli archi: successivamente verrà illustrato come ciò è possibile.