Limitatezza
Una proprietà importante delle reti di Petri è la limitatezza, che indica se le possibili evoluzioni della rete possono essere limitate o illimitate, quindi se gli stati raggiungibili sono in numero finito oppure infiniti. Volendo dare una definizione più formale è possibile dire che una rete posti-transizioni (\(\pt\)) con marcatura \(M\) si dice limitata se e solo se:
$$ \exists k \in \mathbb N, \: \forall M’ ! \in R(\pt, \, M), \: \forall p \in P \quad M’(p) \leq k $$
cioè se esiste un numero naturale \(k\) tale per cui per ogni marcatura \(M’\) raggiungibile da \(M\), per ogni posto \(p\) all’interno della rete il numero di gettoni in quella marcatura raggiungibile è minore o uguale di \(k\) — ovvero se è possibile porre un numero finito tale per cui dopo qualsiasi evoluzione non esista alcun posto che possiede un numero di gettoni maggiore di \(k\) — allora è possibile affermare che la rete è limitata.
Se ciò non si verifica esiste almeno un posto in cui è possibile aumentare tendenzialmente all’infinito il numero di gettoni, tramite una certa evoluzione della rete.
È importante sottolineare che la limitatezza di una rete può dipendere dalla sua marcatura iniziale.
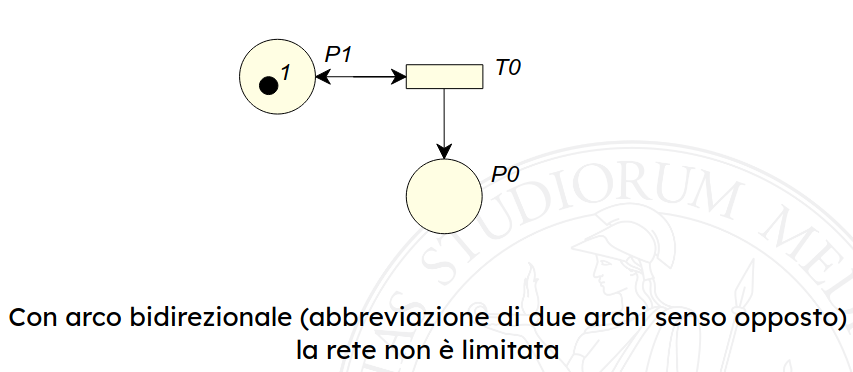
Da reti di Petri a automi
Precedentemente è stato mostrato come a partire da un automa a stati finiti sia possibile ricavare una rete di Petri, ma è possibile fare il contrario? Se la rete è limitata allora l’insieme di raggiungibilità è finito, di conseguenza è possibile definire un corrispondente automa a stati finiti che prende ogni marcatura raggiungibile come un proprio stato e ne traccia le transizioni di stato dell’automa conseguenti alla transizione scattata nella rete di Petri. Due considerazioni:
- gli stati sono le possibili marcature dell’insieme di raggiungibilità;
- le transizioni sono gli eventi che permettono il passaggio da una configurazione alla successiva.
Riuscire a passare dalle reti di Petri agli automi ci permette di modellare un problema in modo più sintetico, ma allo stesso tempo rimane possibile utilizzare i tool di analisi che sfruttano proprietà già consolidate per gli automi. L’unico problema è che questo approccio vale solo per reti limitate.