Capacità dei posti
Inizialmente è stato detto che esistono diversi dialetti riguardanti le reti di Petri. Una possibile estensione consiste infatti nel fissare una capacità massima rispetto al numero di gettoni ammissibili in un posto. Un esempio potrebbe essere quello in cui in un sistema possono essere presenti \(k\) lettori contemporaneamente e non più di \(k\). Avendo la possibilità di definire una capacità dei posti, è facile intuire che diventa possibile forzare la limitatezza della rete.
Tale estensione aumenta la potenza espressiva oppure è semplicemente una scorciatoia? Tramite l’esempio sottostate si può notare che questa estensione non è altro che una tecnica per facilitare la scrittura della rete.
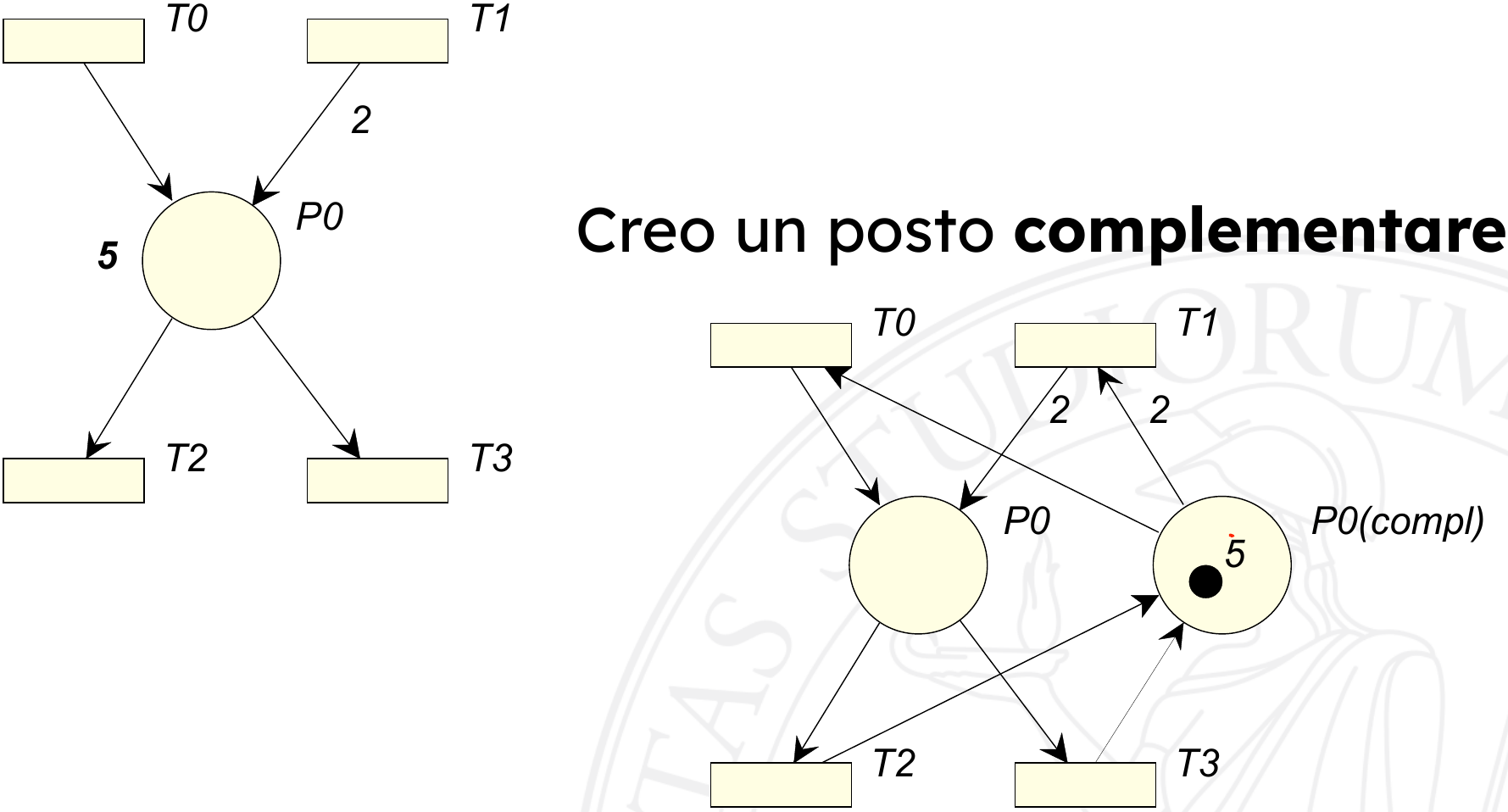
Nella rete con capacità dei posti limitata per far sì che ad esempio la transizione \(t_0\) scatti, è necessario sia che i posti nel suo preset abbiano gettoni sufficienti sia che dopo il suo scatto il posto \(p_0\) non superi il limite assegnatogli. Volendo scrivere la stessa rete utilizzando il metodo classico visto fino ad ora basta aggiungere un posto complementare che quindi rende le reti equipollenti, ossia aventi lo stesso valore espressivo.
Fino a che nel posto complementare esistono dei gettoni, la transizione \(t_0\) può infatti scattare; dal momento però che tutti i gettoni di \(p_0(\text{compl})\) vengono bruciati, \(t_0\) non sarà più abilitata e nel posto \(p_0\) ci sarà il numero massimo di gettoni possibili. Notare come la somma dei gettoni del posto considerato sia esattamente la capacità massima scelta in precedenza.
Questa proprietà vale solo per le reti pure, ovvero le reti che per ogni transizione hanno preset e postset disgiunti.
Posto complementare
Un posto complementare è un posto avente in uscita verso ognuna delle transizioni del posto considerato un arco di ugual peso ma di direzione opposta.
Matematicamente è possibile scivere questa definizione nel seguente modo:
un posto \(pc\) è complementare di \(p\) se e solo se
$$
\begin{align}
\forall t \in T \: \Big [ \exists \langle p, \, t \rangle \in F &\Longleftrightarrow \exists \langle t, \, pc \rangle \in F \quad W(\langle p,, t \rangle) = W(\langle t, \, pc \rangle) \Big ] \\
\land
\forall t \in T \: \Big [ \exists \langle t, \, p \rangle \in F
&\Longleftrightarrow \exists \langle pc, \, t \rangle \in F \quad W(\langle pc, \, t \rangle) = W(\langle t, \, p \rangle) \Big ] .
\end{align}
$$
Per ogni transizione appartenente a \(T\) in uscita da \(p\), quindi tale per cui esiste una relazione di flusso dal posto \(p\) alla transizione \(t\) deve esistere un flusso che va dalla transizione \(t\) al posto complementare \(pc\) avente lo stesso peso.
Inoltre, per le transizioni in ingresso al posto \(p\) (quindi per ogni transizione \(t\) appartenente a \(T\) in ingresso a \(p\)) tali per cui esista un flusso da \(t\) al posto \(p\), deve esistere un flusso che va dal posto complementare \(pc\) a \(t\) di direzione opposta e avente lo stesso peso.
Questa formula garantisce che la somma del numero di gettoni tra il posto e il suo complementare sia costante, permettendo quindi di formulare la condizione di abilitazione (lavorando sul preset della transizione) in modo da dipendere anche dal numero di gettoni presenti nel posto in arrivo.
Abilitazione con capacità
Come è possibile definire la condizione di abilitazione nel caso di reti con capacità sui posti?
La definizione di abilitazione per reti con capacità sui posti è la seguente:
\(t \in T\) è abilitata in \(M\) se solo se:
$$ \begin{align*} \forall p \in \operatorname{Pre}(t) &\quad M(p) \geq W(\langle p, t \rangle) \\ \forall p \in \operatorname{Post}(t) \setminus \operatorname{Pre}(t) &\quad M(p) + W(\langle t, p \rangle) \leq C(p) \\ \forall p \in \operatorname{Post}(t) \cap \operatorname{Pre}(t) &\quad M(p) - W(\langle p, t \rangle) + W(\langle t, p \rangle) \leq C(p). \end{align*} $$
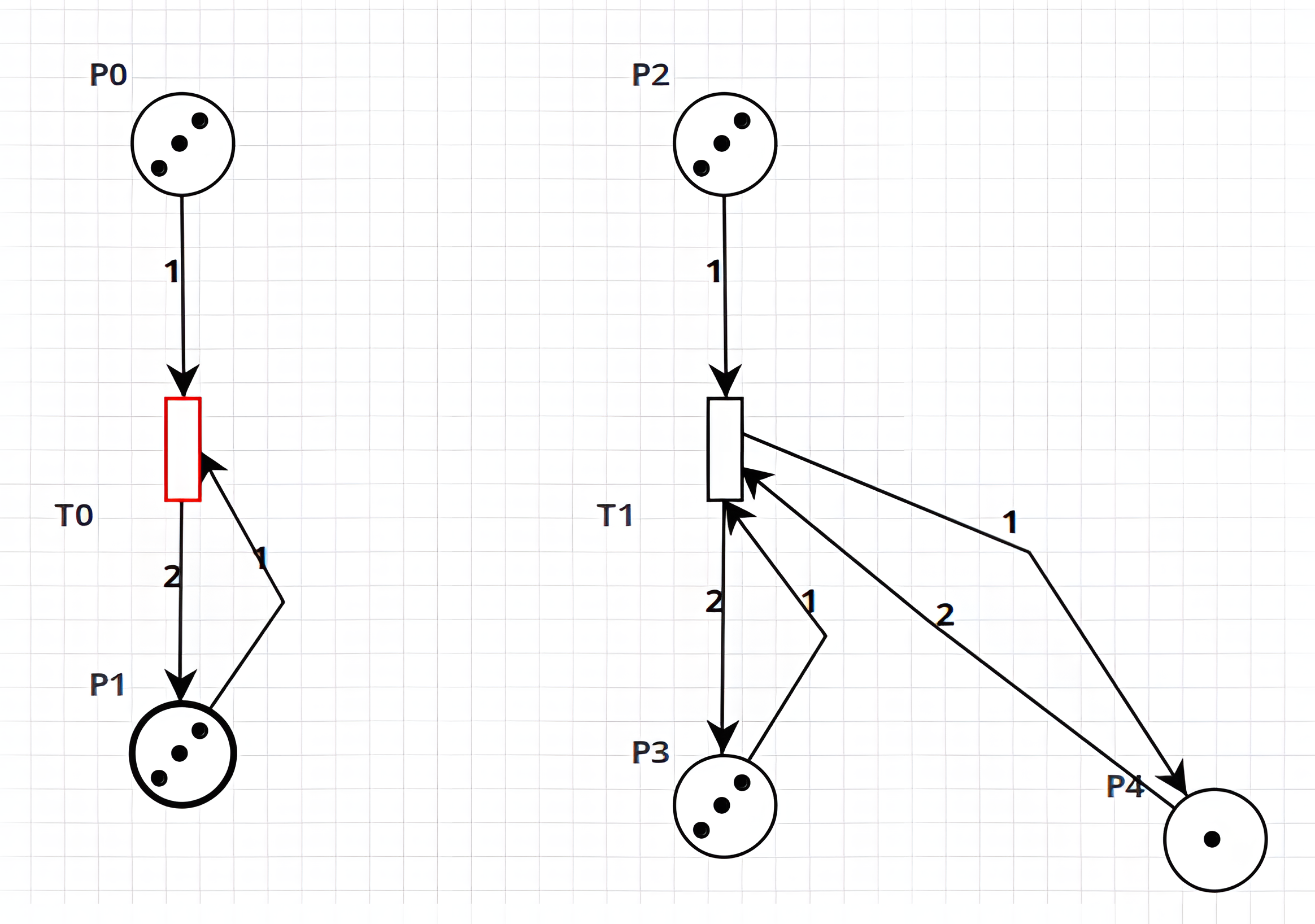
Considerando l’immagine seguente, infatti, possiamo notare come la rete di sinistra abbia ancora una transizione abilitata, mentre quella di destra no.
Nella seconda rete è come se lo scatto venisse spezzato in due fasi: la prima in cui vengono generati i gettoni nel posto (in questo caso \(p_3\)), la seconda invece in cui vengono tolti tanti gettoni quanto è il peso dell flusso da \(p_3\) a \(t_1\).
Nella prima rete invece questo non accade, è come se si verificasse tutto nello stesso istante.
A questo punto, ci si potrebbe chiedere se fosse possibile generare la situazione equivalente nel caso di una rete \(\pt\) classica: la risposta è no, ad eccezione del caso in cui si usano delle reti con posti complementari. Utilizzando i posti complementari è infatti possibile rappresentare solo le reti pure equivalenti, ma non tutte le reti in generale: finché non sono presenti archi in entrata e uscita allo stesso posto dalla stessa transizione non sorge alcun tipo di problema.
Come è possibile superare questa limitazione? Si possono pensare due approcci:
- si trova un altro approccio diverso dai posti complementari;
- si cerca di dimostrare che una rete non pura ha sempre una equivalente rete pura;
quindi, si procede a rimuovere la capacità utilizzando i posti complementari.
Entrambe le soluzioni non sono così immediate.