\(P\)-invarianti
Un \(P\)-invariante è una caratteristica relativa alla marcatura dei posti che non cambia; viene rappresentato da un vettore di pesi \(h\) di dimensione \(\vert P \vert\).
Il vettore \(h\) ricorda la funzione \(H: P \rightarrow \mathbb N \setminus { 0 }\) dalla definizione di rete conservativa, con l’unica differenza che gli elementi di \(h\) possono essere nulli o negativi.
Nel caso in cui un \(P\)-invariante abbia tutti i pesi maggiori di zero allora \(h \equiv H\): la rete sarebbe quindi conservativa e quindi anche limitata.
Tramite l’analisi dei \(P\)-invarianti è quindi possibile stabilire se una rete è conservativa e quindi limitata, fornendo un’alternativa al metodo dell’albero di copertura.
Per ogni marcatura \(m’\) raggiungibile da \(m\), l’invariante è il prodotto vettoriale della marcatura con \(h\).
$$ \forall m’ \text{ raggiungibile da }m \quad hm = hm’ $$
Se \(m’\) è raggiungibile da \(m\), allora esiste una sequenza di scatti ammissibile \(s\) tale per cui
$$ m’ = m + C s, $$
Sostituisco \(m’\) con \(m+Cs\) in \(hm=hm’\) e ottengo \(hm=h(m+Cs)\). Di conseguenza:
$$ hm = h(m + Cs) \\ hm = hm + hCs $$
quindi, semplificando i due \(hm\),
$$ \boxed{hCs = 0}. $$
Ritornando alle assunzioni iniziali, tale proprietà vale solo se esiste una sequenza di scatti ammissibile: le informazioni su \(m\) non sono andate perse.
Nell’ultima formula è presente la matrice \(C\) (nota), il vettore di pesi \(h\) (incognita) e il vettore \(s\) (variabile libera). La relazione vale infatti per ogni sequenza di scatti ammissibile \(s\). La formula precisa è quindi:
$$ \forall s \quad hCs = 0 \ \text{con $s$ rappresentante una sequenza di scatti ammissibile.} $$
Assumendo per un momento che \(hC = 0\), allora qualsiasi sia \(s\) il risultato è sempre zero, perdendo informazione su quest’ultima.
Analogamente, in una rete che possiede una transizione morta la corrispondente posizione in \(s\) sarà sempre zero causando l’azzeramento anche della relativa posizione nel risultato.
Non è quindi necessario che \(hC = 0\) per far sì che \(hCs = 0\), ma è sicuramente sufficiente.
In conclusione, considerando solo \(hC = 0\) è possibile escludere la componente dinamica dalla proprietà ragionando solo in base alle informazioni topologiche (\(C\)) della rete. Trovare l’\(h\) che rende \(hC = 0\) è quindi condizione sufficiente ma non necessaria per cui \(h\) è un \(P\)-invariante, tenendo a mente che esistono comunque \(h\) che non rendono \(hC = 0\) ma potrebbero essere \(P\)-invarianti.
I \(P\)-invarianti determinati con l’espressione \(hC = 0\) non dipendono dalla marcatura iniziale ma solo dalla topologia della rete: se venisse considerato anche \(s\) sarebbero \(P\)-invarianti per qualunque evoluzione della rete a partire dalla marcatura \(m\).
Il sistema \(hC = 0\) è un sistema di equazioni lineare, risolvibile con varie tecniche presentate successivamente.
Copertura di \(P\)-invarianti
Una combinazione lineare di \(P\)-invarianti (e quindi di soluzioni del sistema) è anch’essa un \(P\)-invariante.
Un \(P\)-invariante \(h\) avente tutti i pesi \(\geq 0\) è detta semi-positivo.
Se un posto ha peso positivo in un \(P\)-invariante semi-positivo, allora è limitato nel numero di gettoni massimi che può contenere.
Se così non fosse, infatti, il contributo nella sommatoria vista precedentemente di \(h[i]m[i]\) (con \(h[i] \geq 0\) e \(m[i] > 0\)) sarebbe potenzialmente illimitato.
Se un posto ha peso nullo, potrebbe quindi essere illimitato.
Avere pesi dei posti negativi non fornisce nessuna informazione sulla limitatezza degli stessi nella rete.
Infine, se per ogni posto esiste un \(P\)-invariante semi-positivo il cui peso del posto è positivo, allora la rete è limitata. Matematicamente:
$$
\begin{align*}
&\forall i \in 1..\vert P \vert, \, \exists h \in \mathbb{R}^{\vert P \vert} \quad hC = 0 \land h[.] \geq 0 \land h[i] > 0 \
&\Rightarrow \text{$C$ rappresenta una rete limitata.}
\end{align*}
$$
Si può anche dire che se esiste una combinazione lineare di \(P\)-invarianti tale per cui il \(P\)-invariante risultante è strettamente positivo, allora vuol dire che la funzione \(H : P \rightarrow \mathbb N^+\) (che restituisce proprio quei pesi trovati) è una delle funzioni per cui la rete risulta conservativa.
Esempio
Di seguito è illustrato un esempio sulle proprietà viste dei \(P\)-invarianti.
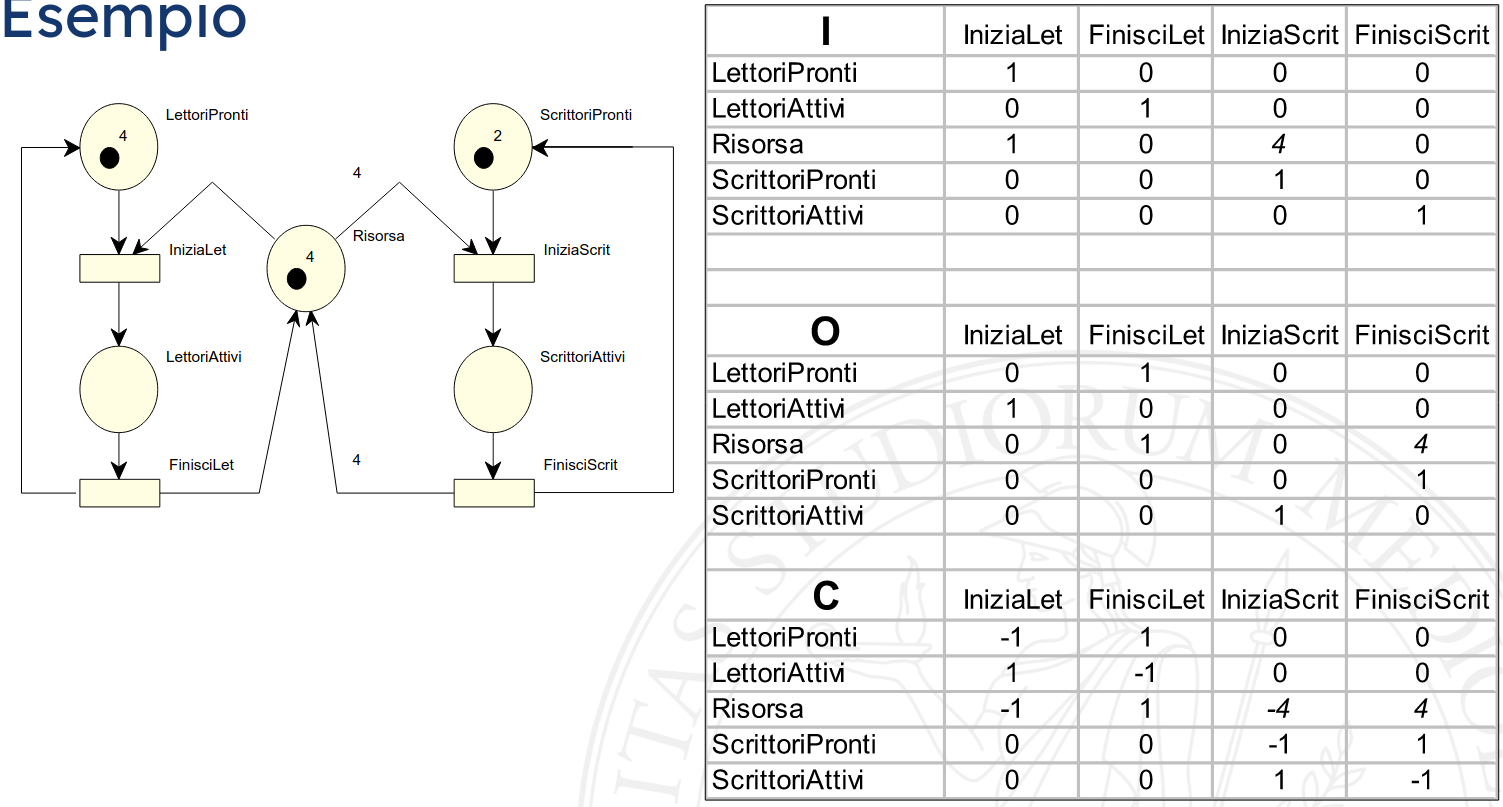
Date le matrici \(I\), \(O\) e \(C = O - I\) sopra è necessario risolvere il sistema \(hC = 0\)
$$ h \begin{bmatrix} -1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \\ -1 & 1 & -4 & 4 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & -1 \end{bmatrix} \! = 0, $$
che si trasforma nel seguente sistema di equazioni lineari:
$$ \begin{cases} -h_0 &+h_1 &-h_2 & & \hphantom{+h_4} = 0 \\ +h_0 &-h_1 &+h_2 & & \hphantom{+h_4} = 0 \\ & &-4h_2 &-h_3 &+h_4 = 0 \ & &+4h_2 &+h_3 &-h_4 = 0. \end{cases} $$
È facilmente notabile che la prima e la seconda equazioni sono uguali a meno di una costante moltiplicativa: sono quindi linearmente dipendenti, insieme alla terza e alla quarta.
Chiedendo quindi a Wolfram|Alpha di risolvere il sistema
$$ \begin{cases} -h_0 &+h_1 &-h_2 & & \hphantom{+h_4} = 0 \\ & &-4h_2 &-h_3 &+h_4 = 0, \end{cases} $$
otteniamo le seguenti basi:
$$ { \langle -1, 0, 1, 0, 4 \rangle, \, \langle 1, 0, -1, 4, 0 \rangle, \, \langle 1, 1, 0, 0, 0 \rangle }, $$
che se combinate linearmente generano infinite soluzioni.
Tra le tre basi ottenute, l’ultima è particolare in quanto ha tutti gli elementi semi-positivi: di conseguenza i posti corrispondenti alle prime due posizioni (con pesi strettamente positivi) sono limitati.
Rimane comunque difficile stabilire se la rete è limitata oppure no.
Algoritmo di Farkas (1902)
E se esistesse un algoritmo che predilige la ricerca di basi minime per un sistema di equazioni, privilegiando quelle semipositive? L’algoritmo in questione è l’algoritmo di Farkas.

Sia \(n\) il numero di righe e \(m\) il numero di colonne della matrice di incidenza \(C\).
L’algoritmo inizia creando una matrice \(D_0\) ottenuta da \(C\) alla quale viene appesa una matrice di identità \(E_n\) di dimensione \(n \cdot n\).
Quindi, per ogni colonna \(i\) da \(1\) a \(m\) si considerano le coppie di righe \(\langle d_1, \, d_2 \rangle\) aventi nella \(i\)-esima riga numeri di segno opposto (non necessariamente uguali in valore assoluto).
Per ogni coppia di righe \(\langle d_1, \, d_2 \rangle\):
- si crea una riga temporanea \(d\) ottenuta combinando linearmente la linea \(d_1\) moltiplicata per il valore assoluto dell’\(i\)-esimo elemento della riga \(d_2\) e sommando il viceversa.
Così facendo, l’\(i\)-esimo argomento della riga \(d\) è uguale a zero; - per evitare instabilità numerica dovuta a numeri troppo grandi si divide \(d\) per il massimo comun divisore dei suoi elementi, assegnando il risultato a \(d’\);
- si estende la matrice \(D_{i-1}\) aggiungendo una nuova ultima riga \(d’\).
Una volta terminato il ciclo sulla coppia di righe, si scartano tutte le righe della matrice \(D_{i-1}\) cui \(i\)-esimo elemento è diverso da \(0\). Infine, al termine del ciclo esterno si eliminano le prime \(m\) colonne di \(D_{m}\), essendo azzerate. Nella matrice risultante (corrispondente alla matrice \(E_n\)) sono presenti i \(P\)-invarianti.
Continuazione dell’esempio con Farkas
Nell’esempio iniziato in precedenza si era arrivati ad un punto in cui si necessitava ottenere basi semi-positive e quindi \(P\)-invarianti semi-positivi: per fare ciò si può applicare l’algoritmo sopra descritto.
Si inizia creando la matrice \(D_0 = [C \: \vert \: E_n]\):
$$ D_0 = \begin{bmatrix} -1 &1 &0 &0 &1 &0 &0 &0 &0 \\ 1 &-1 &0 &0 &0 &1 &0 &0 &0 \\ -1 &1 &-4 &4 &0 &0 &1 &0 &0 \\ 0 &0 &-1 &1 &0 &0 &0 &1 &0 \\ 0 &0 &1 &-1 &0 &0 &0 &0 &1 \end{bmatrix}. $$
Osservando la prima colonna (\(i = 1\)) si nota che sono presenti due coppie di righe aventi segno opposto: la prima e la seconda, la seconda e la terza.
A questo punto si possono combinare linearmente le coppie appendendo i risultati come ultima riga:
$$ D_0 = \begin{bmatrix} -1 &1 &0 &0 &1 &0 &0 &0 &0 \\ 1 &-1 &0 &0 &0 &1 &0 &0 &0 \\ -1 &1 &-4 &4 &0 &0 &1 &0 &0 \\ 0 &0 &-1 &1 &0 &0 &0 &1 &0 \\ 0 &0 &1 &-1 &0 &0 &0 &0 &1 \\ 0 &0 &0 &0 &1 &1 &0 &0 &0 \\ 0 &0 &-4 &4 &0 &1 &1 &0 &0 \end{bmatrix}. $$
Le prime tre righe contengono nella colonna \(i\)-esima (la prima) elementi non nulli; si scartano:
$$ D_1 = \begin{bmatrix} 0 &0 &-1 &1 &0 &0 &0 &1 &0 \\ 0 &0 &1 &-1 &0 &0 &0 &0 &1 \\ 0 &0 &0 &0 &1 &1 &0 &0 &0 \\ 0 &0 &-4 &4 &0 &1 &1 &0 &0 \end{bmatrix}. $$
Si procede iterativamente senza ulteriori azioni fino alla terza colonna, dove sono presenti due coppie di righe aventi segni opposti in posizione \(i\): la prima e la seconda, la prima e la quarta.
Applicando gli stessi passaggi di prima, la matrice \(D_3\) che si ottiene è la seguente:
$$ D_3 = \begin{bmatrix} 0 &0 &0 &0 &1 &1 &0 &0 &0 \\ 0 &0 &0 &0 &0 &1 &1 &0 &4 \\ 0 &0 &0 &0 &0 &0 &0 &1 &1 \end{bmatrix}. $$
Infine, considerando la matrice \(D_m\) senza le prime colonne nulle, si ottengono le seguenti basi di \(h\):
$$ { \langle 1, 1, 0, 0, 0 \rangle, \, \langle 0, 1, 1, 0, 4 \rangle, \, \langle 0, 0, 0, 1, 1 \rangle }. $$
Interpretazione dei risultati ottenuti
È facile notare come la rete sia limitata, in quanto per ogni posizione (posto) esiste almeno un \(P\)-invarianti semipositivi cui valore in tale posizione è strettamente positivo.
Conoscendo ora possibili valori per \(h\), nella relazione \(hm = hm_0\) l’unica incognita al momento è \(m\): la marcatura generica che è possibile raggiungere.
Considerando il primo \(P\)-invariante \(h_1 = \langle 1, 1, 0, 0, 0 \rangle\) e la marcatura iniziale \(m_0 = \langle 4, 0, 4, 2, 0 \rangle\) si ottiene la relazione \(h_1m = hm_0 = 4\) riguardante i seguenti posti:
$$ \text{LettoriPronti} + \text{LettoriAttivi} = 4. \tag{$h_1$} $$
I posti cui peso è \(1\) (proveniente da \(h_1\)) sono \(\text{LettoriPronti}\) e \(\text{LettoriAttivi}\), mentre il \(4\) dipende dal numero di gettoni in \(\text{LettoriPronti}\) in \(m_0\): la somma dei due è garantita essere costante.
In generale, i termini a sinistra dipendono da \(h\), quelli a destra da \(m_0\).
Per \(h_2 = \langle 0, 0, 0, 1, 1 \rangle\) il procedimento è lo stesso:
$$ \text{ScrittoriPronti} + \text{ScrittoriAttivi} = 2. \tag{$h_2$} $$
Il terzo risultato, per \(h_3 = \langle 0, 1, 1, 0, 4 \rangle\) è il più interessante:
$$ \text{LettoriAttivi} + \text{Risorsa} + 4 \cdot \text{ScrittoriAttivi} = 4 \tag{$h_3$}. $$
In tutti i risultati è implicito che tutti gli operandi devono essere interi maggiori o uguali a zero.
Con dell’algebra è possibile riscrivere l’ultimo risultato (\(h_3\)) nel seguente modo:
$$ \begin{align} \frac{4 \cdot \text{ScrittoriAttivi}}{4} &= \frac{4 - \text{LettoriAttivi} - \text{Risorsa}}{4} \\ \text{ScrittoriAttivi} &= 1 - \frac{\text{LettoriAttivi}}{4} -\frac{\text{Risorsa}}{4} \\ \text{ScrittoriAttivi} &= 1 - \frac{\text{LettoriAttivi} + \text{Risorsa}}{4}. \end{align} $$
Dall’ultima espressione è possibile determinare che gli \(\text{ScrittoriAttivi}\) sono o zero o uno, in quanto \(\frac{\text{LettoriAttivi} + \text{Risorsa}}{4}\) è necessariamente positivo.
A questo punto “LettoriAttivi” + “Risorsa” si sa essere un valore positivo, che diviso per 4 rimane un numero positivo, a meno che non siano entrambi 0.
È quindi garantito matematicamente che gli scrittori sono in mutua esclusione.
Procedendo similmente per i lettore, si ottiene che:
$$ \text{LettoriAttivi} = 4 \cdot (1 - \text{ScrittoriAttivi}) - \text{Risorsa}. $$
Si può quindi concludere che:
- \(\text{ScrittoriAttivi} \leq 1\);
- \(\text{LettoriAttivi} \leq 4\);
- \(\text{LettoriAttivi} > 0 \Longrightarrow \text{ScrittoriAttivi} = 0\);
- \(\text{ScrittoriAttivi} > 0 \Longrightarrow \text{LettoriAttivi} = 0\).