Concorrenza

È in qualche modo intuitivo considerare la relazione di concorrenza come la relazione opposta alla relazione di conflitto: due transizioni \((t_1, \, t_2)\) sono in:

• concorrenza strutturale \(\Longleftrightarrow \operatorname{Pre}(t_1) \cap \operatorname{Pre}(t_2) = \varnothing\);
• concorrenza effettiva in una marcatura \(M \Longleftrightarrow\)
  • \(\boxed{M \ [ \ t_1 >} \land \boxed{M \ [ \ t_2 >}\);
  • \(\forall p \in \operatorname{Pre}(t_1) \cap \operatorname{Pre}(t_2) \quad M(p) \geq W(\langle p, \, t_1 \rangle) + W(\langle p, \, t_2\rangle)\).

Quest’ultima formula indica che due identificatori delle transizioni sono in concorrenza effettiva se e solo se per tutti i posti che hanno in comune c’è un numero di gettoni sufficienti per farle scattare entrambe.

In questo caso non esiste alcun legame tra concorrenza strutturale ed effettiva, diversamente da quanto abbiamo visto in precedenza per le relazioni di conflitto. Se si verificano le condizioni per avere una concorrenza strutturale è possibile che le due transizioni non siano abilitate, oppure se si verificano le condizioni per avere concorrenza effettiva è possibile che \(t_1\) e \(t_2\) abbiano posti in comune che posseggano abbastanza gettoni per entrambe.

Questo però non esclude il fatto che sia possibile avere concorrenza strutturale ed effettiva contemporaneamente, infatti di seguito sono riportati degli esempi che confermano ciò:

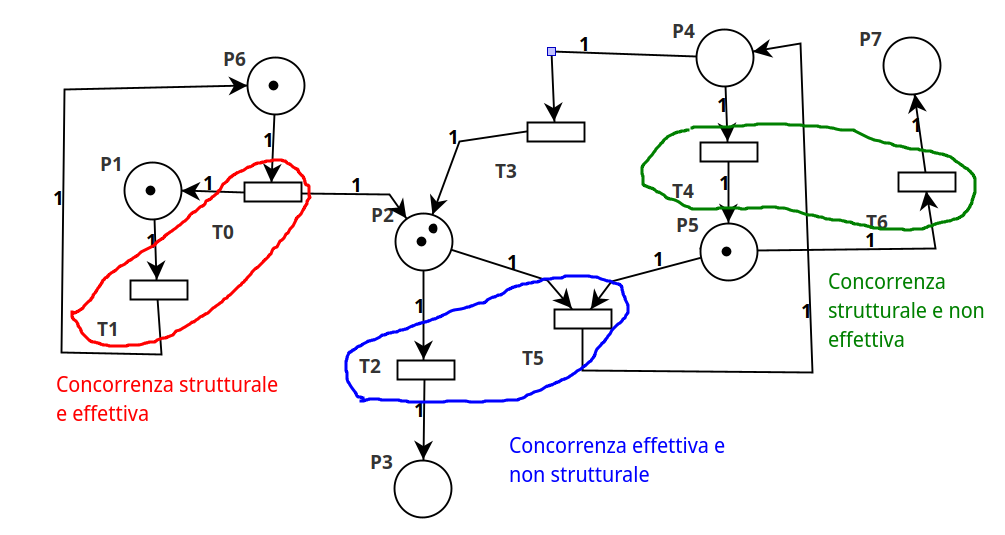
Ovviamente è anche possibile che non ci sia alcun tipo di concorrenza: è sufficiente che due transizioni abbiano in comune un posto e una delle due non sia abilitata.