Semantica temporale forte (STS)

Finora abbiamo lasciato aperta la possibilità che una transizione pur potendo scattare non lo facesse. Questa alternativa non è però contemplata in molti modelli temporizzati, in cui il determinismo gioca un forte ruolo: spesso si vuole che se una transizione può scattare, allora deve scattare entro il suo massimo tempo di scatto ammissibile.

Per forzare questo comportamento viene creata una semantica temporale apposita, che prende il nome di semantica temporale forte (Strong Time Semantic, STS): essa impone che una transizione deve scattare ad un suo possibile tempo di scatto a meno che non venga disabilitata prima del proprio massimo tempo di scatto ammissibile. Aggiungere quest’ultima clausola permette alle transizioni di non dover prevedere il futuro: se esse fossero programmate per scattare in un certo istante ma prima di esso lo scatto di un’altra transizione le disabilitasse non si richiederebbe che esse tornino indietro nel tempo per scattare all’ultimo istante di tempo utile.

Essendo un ulteriore irrigidimento rispetto alla semantica temporale monotonica debole, la STS dovrà sia rispettare gli assiomi A1, A2 e A3, sia la seguente nuova coppia di assiomi, che porta il totale a cinque:

• (A4) Marcatura forte iniziale: il massimo tempo di scatto di tutte le transizioni abilitate nella marcatura iniziale dev’essere maggiore o uguale del massimo timestamp associato ad un gettone in tale marcatura.
  Questo assicura cioè che la marcatura iniziale sia consistente con la nuova semantica temporale: un gettone dotato di timestamp superiore al tempo di scatto massimo di una transizione abilitata non sarebbe potuto essere generato prima che la transizione scattasse (cosa che deve fare!), rendendo quindi la marcatura in questione non più quella iniziale.

• (A5) Sequenza di scatti forte: una sequenza di scatti ammissibile in semantica MWTS che parta da una marcatura forte iniziale è una sequenza di scatti forte se per ogni scatto il tempo di scatto della transizione non è maggiore del massimo tempo di scatto di un’altra transizione abilitata.
  Si sta cioè accertando che ogni transizione scatti entro il suo tempo massimo se non viene disabilitata prima da un altro scatto: per fare ciò, si permette alle transizioni di scattare solo se non ci sono altre transizioni abilitate che sarebbero già dovute scattare, costringendo quindi queste ultime a farlo per far continuare a evolvere la rete.

Ecco dunque che sequenze di scatto che soddisfano gli assiomi A1, A2, A3, A4 e A5 vengono dette sequenze ammissibili in semantica forte.

STS \(\not\equiv\) MWTS

In virtù dell’ultimo assioma si potrebbe pensare che esista un modo per trasformare ogni sequenza di scatti MWTS in una sequenza STS, realizzando così un’equivalenza. Purtroppo, però, non è così: una sequenza STS è sempre anche MWTS, ma non è sempre vero il contrario.

Poiché infatti non è più possibile a causa dell’assioma A2 riordinare le sequenze per ottenerne altre di equivalenti, è possibile trovare numerose sequenze che sono MWTS ma non STS. Riprendendo la rete già vista in precedenza e assumendo anche in questo caso dei timestamp iniziali nulli per i gettoni:

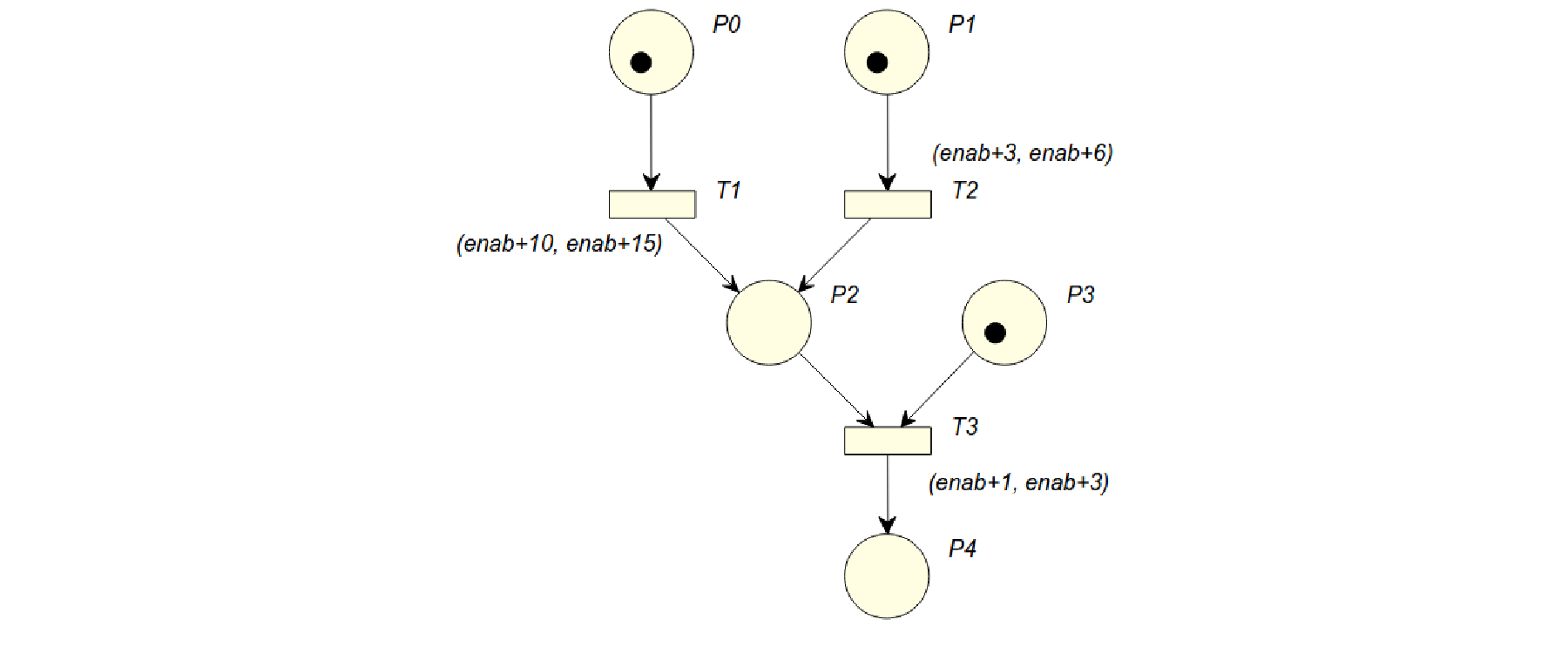
è facile vedere che la sequenza ammissibile in semantica monotonica debole:

$$ \text{T2 scatta al tempo 6} \rightarrow \text{T1 scatta al tempo 12} \rightarrow \text{T3 scatta al tempo 14} $$

non è invece una sequenza ammissibile in semantica forte, in quanto lo scatto di T2 abilita la transizione T3, che dovrebbe quindi scattare entro il tempo 9 (\(enab = 6\)) ma non lo fa.