Definizioni

Definizione informale

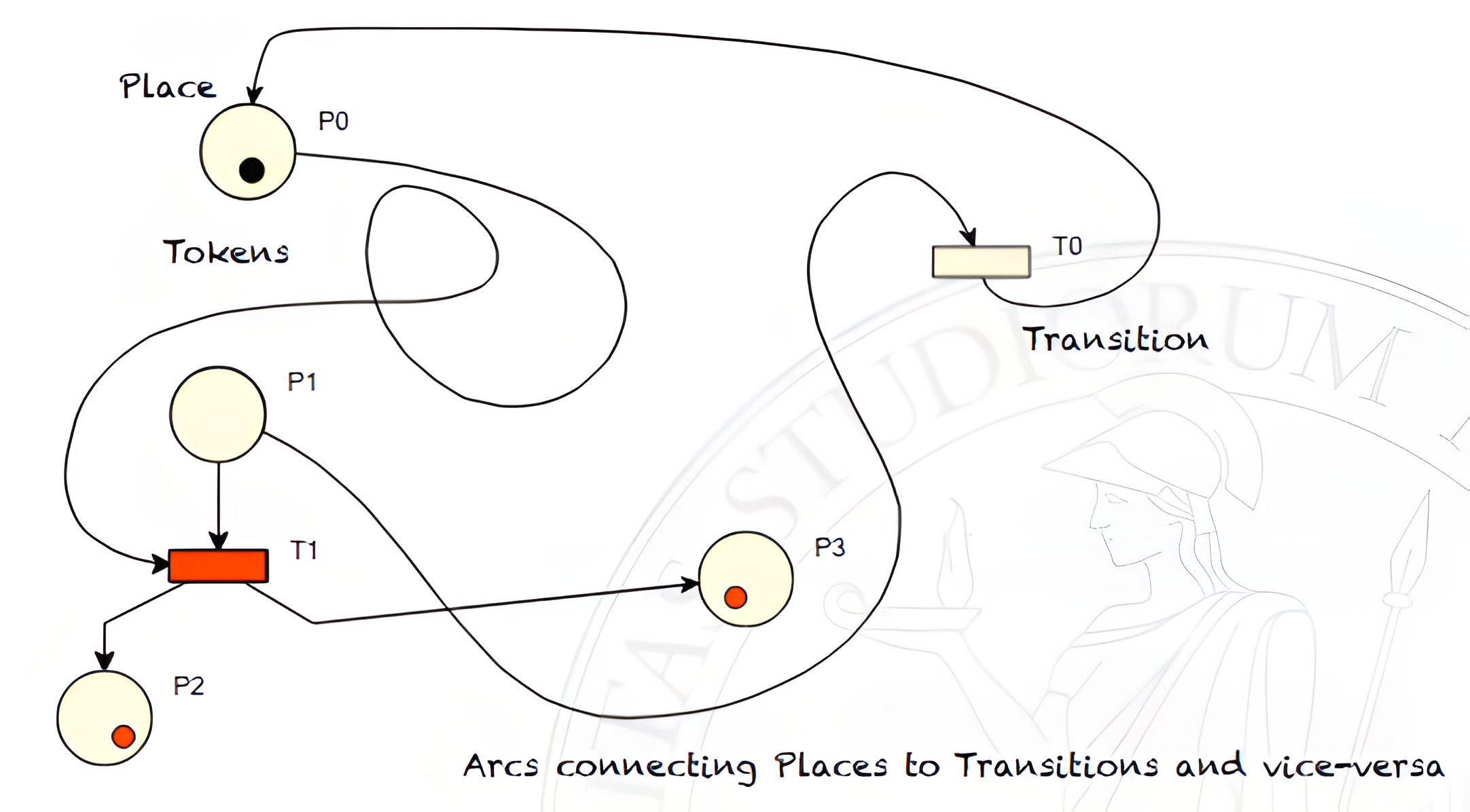
Un vantaggio delle reti di Petri è che possono essere viste in maniera informale dal cliente. È infatti facile rappresentare una rete di Petri come un grafo in cui ogni nodo rappresenta o un posto o una transizione e gli archi i collegamenti presenti tra le transizioni e i posti. Il grafo è bipartito, ovvero un grafo in cui nodi di un tipo sono messi in relazione solo con nodi dell’altro tipo: in questo caso i posti possono essere collegati soltano a transizioni e viceversa.

Ad ogni posto è assegnato un certo numero di gettoni (o token) – sarà successivamente approfondito il senso dell’assegnamento di un numero infinito di gettoni a un posto.

La disposizione dei gettoni nei posti in un dato momento all’interno della rete di Petri ne determina il suo stato complessivo.

Per far evolvere lo stato della rete, l’assegnamento dei gettoni deve poter variare.
La trasformazione dello stato è effettuata dallo scatto di una transizione:

• una transizione si dice abilitata (enabled) quando la somma dei gettoni dei posti collegati ingresso è maggiore di un certo numero;
• una transizione scatta (fire) quando, dopo essere stata abilitata, consuma i gettoni dei posti collegati in ingresso e ne genera altri all’interno dei posti collegati in uscita. È importante notare come i gettoni non si spostano da un posto a un altro conseguentemente a uno scatto, ma vengono distrutti nei posti in ingresso alla transizione e generati nei posti in uscita. Quest’ultima considerazione è importante per capire che i gettoni non sono necessariamente sempre dello stesso numero in ingresso e in uscita.

Tramite questo modello operativo è facile mostrare al cliente quando qualcosa cambia all’interno del sistema, perché risulta più intuitivo rispetto a un linguaggio logico e descrittivo.

Lo svantaggio è che fornisce informazioni parziali su come il sistema compie le azioni che dovrebbe eseguire, rischiando di essere una via di mezzo tra specifica e documento di design. Si può comunque chiamare specifica perché viene definito totalmente e inequivocabilmente il comportamento del sistema.

La rete descritta è quindi una macchina di riferimento da utilizzare come confronto per stabilire la validità del sistema sotto esame, come se fosse un oracolo.

Definizione matematica

Come già detto, esistono numerosi dialetti di reti di Petri. In questo caso vediamo le PT net (reti con posti e transizioni) che sono le più classiche, successivamente verranno descritte delle estensioni e riduzioni di queste reti.

Una rete di Petri classicamente è una 5-tupla \([P, \, T; \; F, \, W, \, M_0]\) in cui:

• \(P\) è l’insieme degli identificatori dei posti;
• \(T\) è l’insieme degli identificatori delle transizioni;
• \(F\) è l’insieme delle relazioni di flusso;
• \(W\) è una funzione che associa un peso ad ogni flusso;
• \(M_0\) è la marcatura iniziale, ovvero l’assegnamento iniziale dei gettoni.

In generale definiamo come marcatura una particolare configurazione dell’assegnamento dei gettoni all’interno della rete di Petri, sia essa iniziale o una sua evoluzione.

Da notare che \(P\) e \(T\) a livello matematico sono degli insiemi di identificatori che non si sovrappongono (dato che si tratta di entità differenti) a cui poi verrà assegnato un significato, quindi precedentemente sono stati associati a posti e transizioni, ma di fatto sono tutti identificatori.

Data la 5-tupla appena descritta esistono le seguenti proprietà:

• \(P \cap T = \varnothing\);
• \(P \cup T \neq \varnothing\) (una rete in cui non c’è nulla non è una rete: almeno un posto o una transizione ci devono essere);
• \(F \subseteq (P \times T) \cup (T \times P)\);
• \(W: : F \rightarrow \mathbb N \setminus { 0 }\);
• \(M_0: P \rightarrow \mathbb N\).

Utilizziamo inoltre alcune scorciatoie:

• \(\operatorname{Pre}(a) = { d \in (P \cup T) \quad \langle d, \, a \rangle \in F }\).
  Il preset di un nodo \(a\) è l’insieme degli elementi \(d\) appartenenti all’unione degli insiemi degli identificatori di posti e transizioni tali che esiste una relazione di flusso tra \(d\) e \(a\) appartenente a \(F\). \ In sostanza questo insieme rappresenta l’insieme degli identificatori antecedenti ad \(a\);
• \(\operatorname{Post}(a) = { d \in (P \cup T) \quad \langle a,, d \rangle \in F }\).
  Il postset di un nodo \(a\) è l’insieme degli elementi \(d\) appartenenti all’unione degli insiemi degli identificatori di posti e transizioni tali che esiste una relazione di flusso tra \(a\) e \(d\) appartenente a \(F\). \ In sostanza questo insieme rappresenta l’insieme degli identificatori successivi ad \(a\).

Tutto questo rappresenta la parte statica delle reti di Petri, ovvero quando vengono osservate in un preciso istante di tempo, senza considerare i cambiamenti che potrebbero avvenire al suo interno.

Comportamento dinamico

Una transizione \(t \in T\) è abilitata in una particolare marcatura \(M\) se e solo se

$$ \boxed{ \forall p \in \operatorname{Pre}(t) \quad M(p) \geq W( \langle p, \, t \rangle ) }. $$

In notazione, \(\boxed{M \ [ \ t >}\) significa che \(t\) è abilitata in \(M\).

Significa che per ogni elemento collegato in ingresso a \(t\) esiste un numero di gettoni maggiore del peso dell’arco che collega \(p\) a \(t\). Un aspetto interessante di questa definizione è che non si sta ragionando su tutti i posti della rete, ma solo su quelli collegati in ingresso a \(t\). Di conseguenza, non è necessario conoscere l’intera rete per poter affermare che una transizione sia abilitata o meno, ma è sufficiente controllare la zona che comprende i posti appartenenti a \( \operatorname{Pre}(a) \). Questa proprietà è chiamata località dell’analisi.

Lo scatto di una transizione \(t \in T\) in una particolare marcatura \(M\) produce nel momento successivo una nuova marcatura \(M’\) tale per cui

$$ \begin{aligned} \forall p \in \operatorname{Pre}(t) \setminus \operatorname{Post}(t) &\quad M’(p) = M(p) - W(\langle p, \, t \rangle); \\ \forall p \in \operatorname{Post}(t) \setminus \operatorname{Pre}(t) &\quad M’(p) = M(p) + W(\langle t, \, p \rangle); \\ \forall p \in \operatorname{Post}(t) \cap \operatorname{Pre}(t) &\quad M’(p) = M(p) - W(\langle p, \, t \rangle) + W(\langle t, \, p \rangle); \\ \forall p \in P - \left ( \operatorname{Post}(t) \cup \operatorname{Pre}(t) \right ) &\quad M’(p) = M(p). \end{aligned} $$

Specificando in modo descrittivo le notazioni precedenti:

• per ogni identificatore \(p\) appartenente al preset ma non al postset della transizione \(t\), il numero di gettoni della nuova marcatura \(M’\) sarà uguale al numero di gettoni della marcatura precedente \(M\) meno il peso dell’arco che collega \(p\) a \(t\);
• per ogni identificatore \(p\) appartenente al postset ma non al preset della transizione \(t\), il numero di gettoni della nuova marcatura \(M’\) sarà uguale al numero di gettoni della marcatura precedente \(M\) più il peso dell’arco che collega \(t\) a \(p\);
• per ogni identificatore \(p\) appartenente sia al preset sia al postset della transizione \(t\), il numero di gettoni della nuova marcatura \(M’\) sarà uguale al numero di gettoni della marcatura precedente \(M\) meno il peso dell’arco che collega \(p\) a \(t\) più il peso dell’arco che collega \(t\) a \(p\);
• per ogni identificatore \(p\) appartenente all’insieme dei posti meno l’unione tra preset e postset di \(p\) la marcatura non cambia.

In notazione, \(\boxed{\boxed{M \ [ \ t >} \, M’}\) significa che lo scatto di \(t\) in \(M\) produce \(M’\).

È importante notare come una transizione può scattare nel caso in cui non abbia alcun elemento nel suo preset; questo significa che la transizione in questione non possiede prerequisiti per scattare.