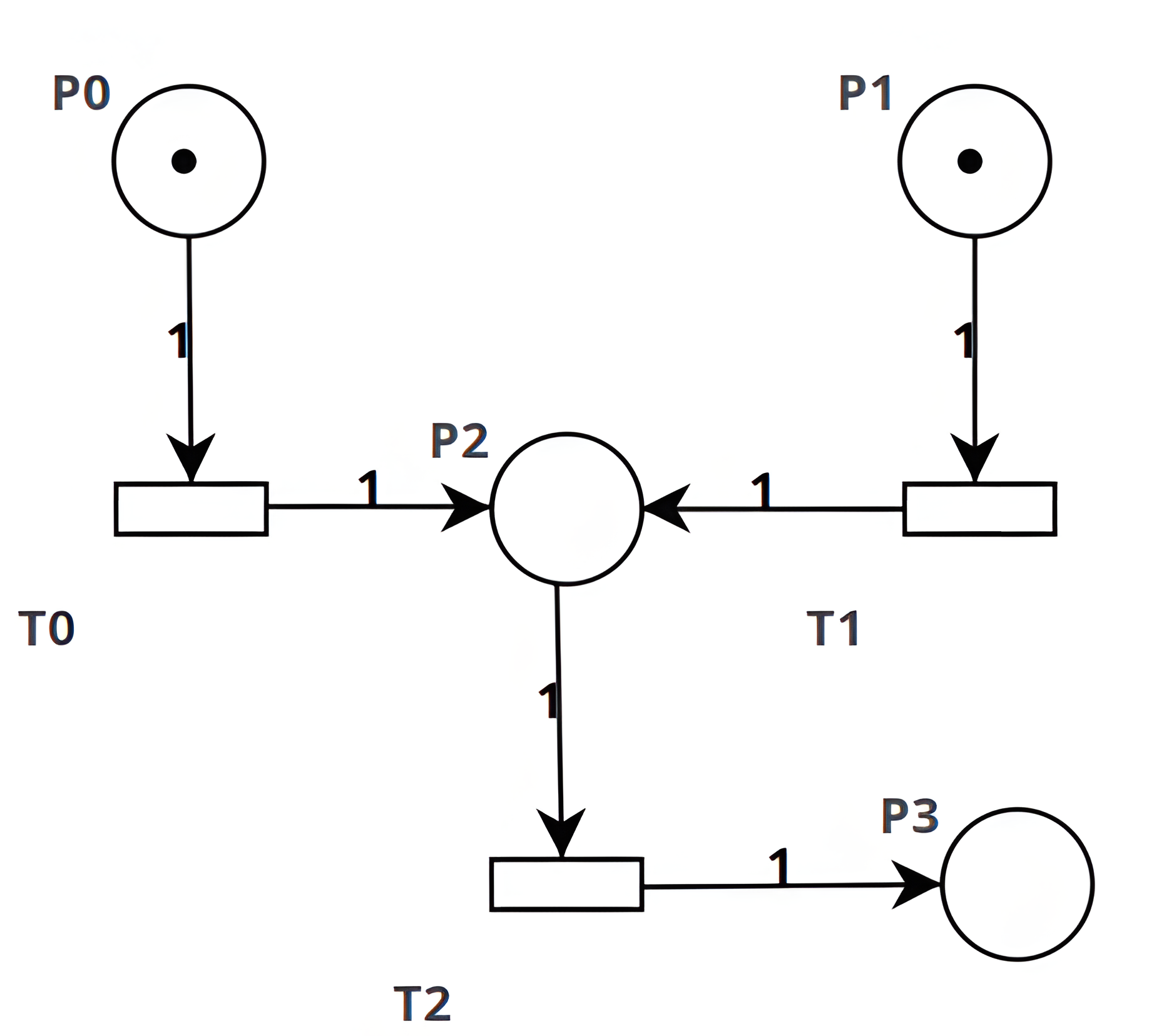
Sequenza
Una transizione \(t_1\) è in sequenza con una transizione \(t_2\) in una marcatura \(M\) se e solo se
$$\boxed{M \ [ \ t_1 >} \: \land \: \lnot \, \boxed{ M \ [ \ t_2 > } \: \land \: \boxed{ M \ [ \ t_1 t_2 > } \, .$$
Questa formula indica che:
- \(t_1\) è abilitata in \(M\);
- \(t_2\) NON è abilitata in \(M\);
- \(t_2\) viene abilitata dallo scatto di \(t_1\) in \(M\).
Si può notare una relazione d’ordine non simmetrica in cui lo scatto di \(t_1\) è una condizione sufficiente per cui \(t_2\) possa scattare: questo tipo di relazione permette quindi di creare un ordine di scatto delle transizioni. È condizione sufficiente e non necessaria perchè osservando l’esempio sottostante è facile capire che lo sacatto di \(t_0\) non è necessario per far si che \(t_2\) scatti: infatti anche se dovesse avvenire lo scatto di \(t_2\), la transizione \(t_1\) diventerebbe comunque abilitata.