Semantica temporale monotonica debole (MWTS)

Come i più attenti avranno notato, nell’elencare gli assiomi necessari per la semantica temporale debole abbiamo saltato un ipotetico assioma A2. Ebbene, ciò non è un caso: esiste infatti un’estensione della semantica WTS che aggiunge tra i propri requisiti il rispetto di tale assioma.

Si tratta della semantica temporale monotonica debole (Monotonic WTS, MWTS), e differisce dalla semantica WTS perché impone necessariamente che i tempi di scatto delle transizioni all’interno di una sequenza siano monotoni non decrescenti, forzando così il fatto che nell’intera rete il tempo non possa tornare indietro.
Più formalmente, la semantica introduce il seguente assioma:

• (A2) Monotonicità dei tempi di scatto di una sequenza: tutti i tempi di scatto di una sequenza di scatti devono essere ordinati nella sequenza in maniera monotonicamente non decrescente (\(\geq\)).
  Anche questo serve a garantire la proprietà intuitiva di consistenza, evitando cioè che il tempo torni indietro. Non richiedendo però che i tempi siano disposti in modo strettamente crescente ma ammettendo che nella sequenza lo stesso tempo sia ripetuto si lascia aperta la possibilità che nella rete più transizioni scattino in contemporanea, oppure che due transizioni scattino in tempi talmente ravvicinati che la granularità temporale del modello non è in grado di rilevare la differenza.

Le sequenze di scatti che soddisfano gli assiomi A1, A2 e A3 vengono dette sequenze ammissibili in semantica monotonica debole.
Sebbene sembri una differenza da nulla, imporre la monotonicità dei tempi di scatto ha in realtà ripercussioni piuttosto grandi: in una rete che segue la MWTS quando si analizzano gli scatti è necessario non solo fare un’analisi locale del preset e del tempo di abilitazione e scatto della transizione, ma anche assicurarsi che non ci sia nessuna transizione nella rete in grado di scattare prima. Si perde cioè la caratteristica di località, introducendo la necessità di mantenere un’informazione comune sull’ultimo scatto nella rete.

WTS \(\equiv\) MWTS

Fortunatamente per noi esiste un teorema che afferma che per ogni sequenza di scatti ammissibile in semantica debole \(S{WTS}\) esiste una sequenza di scatti ammissibile in semantica monotonica debole \(S_{MWTS}\) equivalente ottenibile per semplice permutazione delle occorrenze degli scatti._

Non si tratterà di sequenze uguali, ma entrambe le sequenze produrranno la stessa marcatura finale. Questo è un enorme vantaggio, in quanto ciò ci permette di infischiarcene della monotonicità degli scatti durante l’analisi della rete, potendo così sfruttare la località e conseguentemente le tecniche di analisi per le reti di Petri (ad alto livello) già viste in precedenza.

Esempio di traduzione

Si prenda in esame la rete in figura:

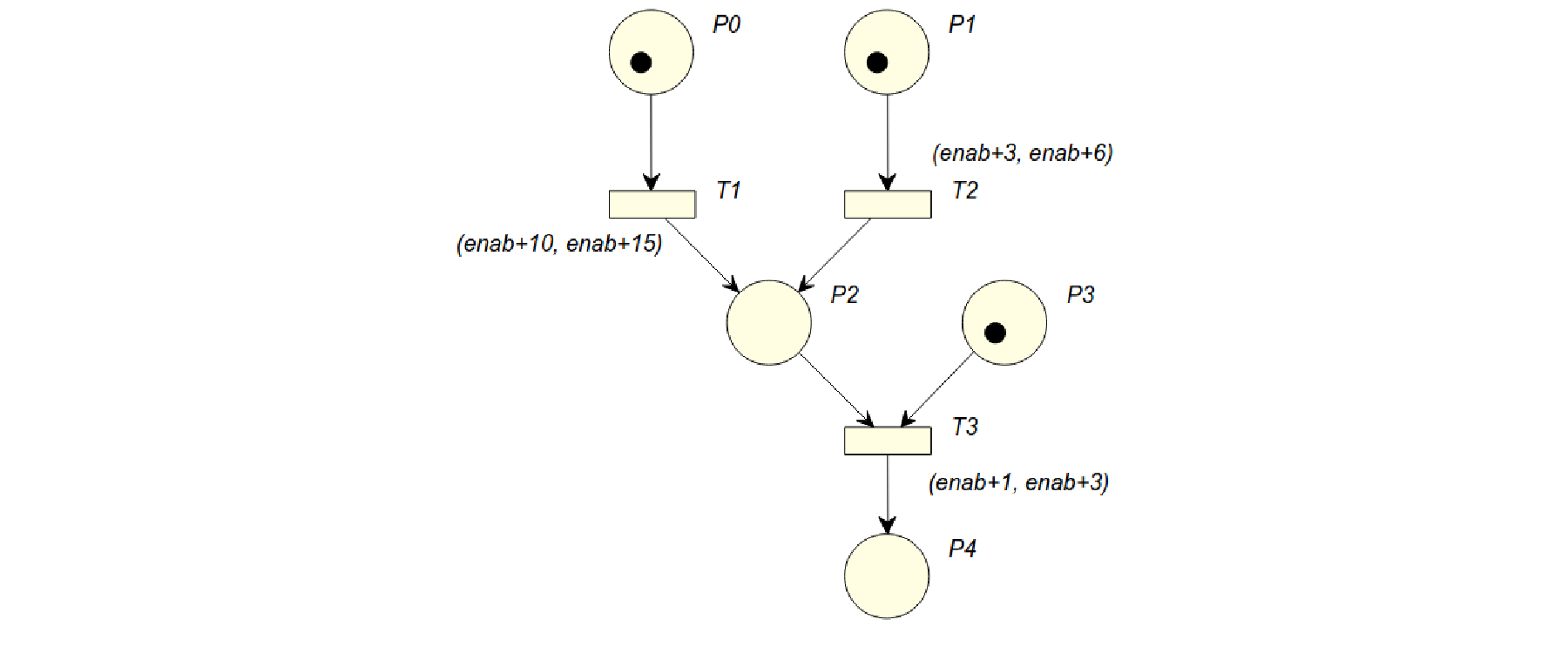
Assumendo i timestamp iniziali di tutti i gettoni uguali a zero, si consideri la seguente sequenza ammissibile WTS di scatti:

$$ \text{T1 scatta al tempo 12} \rightarrow \text{T3 scatta al tempo 14} \rightarrow \text{T2 scatta al tempo 4} $$

Tale sequenza non rispetta la monotonicità, in quanto T2 scatta “nel passato” dopo lo scatto di T3, e produce la marcatura \(\langle0, 0, 1, 0, 1\rangle\). Tuttavia, riordinando la sequenza come:

$$ \text{T2 scatta al tempo 4} \rightarrow \text{T1 scatta al tempo 12} \rightarrow \text{T3 scatta al tempo 14} $$

è possibile ottenere una marcatura identica ma con una sequenza che rispetta ora la monotonicità, essendo cioè ammissibile in semantica temporale monotonica debole.