Reti Time Basic

Prima di darne una vera e propria definizione matematica iniziamo a introdurre le reti Time Basic (TB) in modo informale.

Introdotte per la prima volta da Ghezzi e dai suoi collaboratori nel 1989, le reti TB associano insiemi variabili di tempi di scatto assoluti alle transizioni: ciascuna transizione possiede cioè un insieme di tempi in cui potrebbe scattare, definito in maniera dinamica a seconda dello stato. Tali tempi di scatto potrebbero poi essere definiti sia in termini assoluti che in termini dei tempi associati ai gettoni.

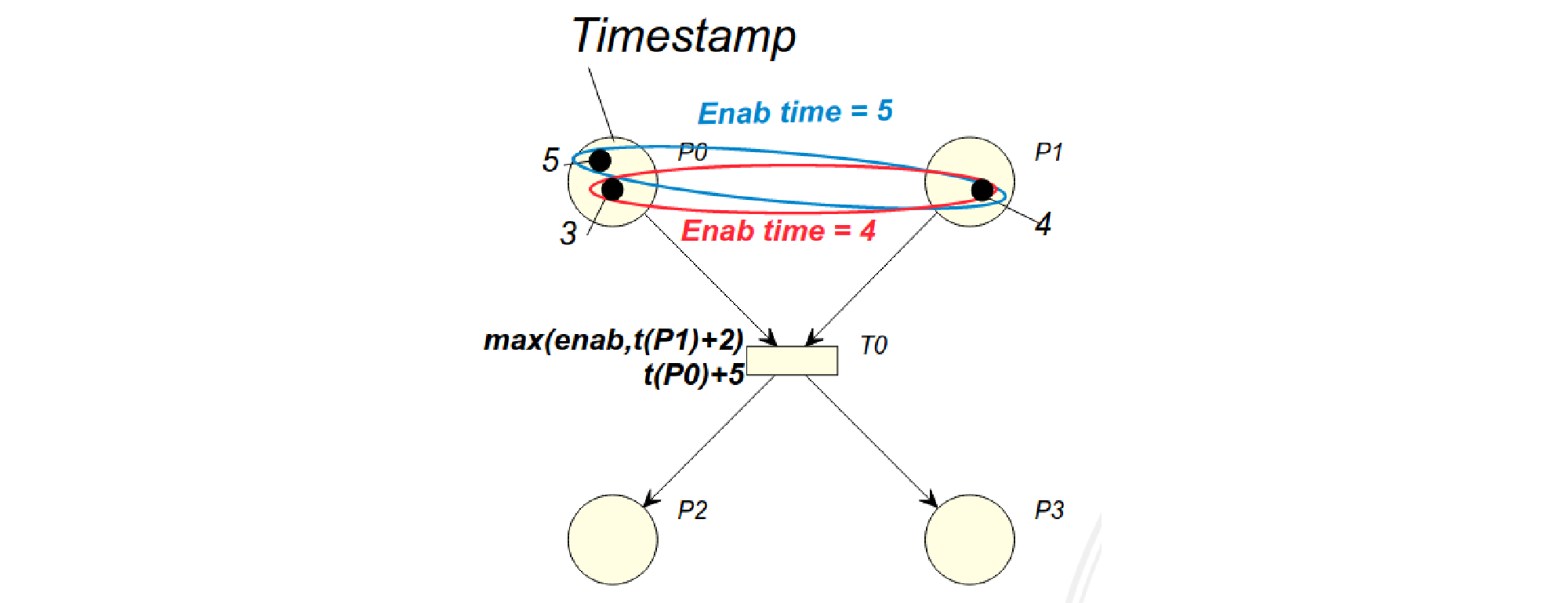
Nelle reti TB infatti i gettoni non sono più anonimi, ma caratterizzati ciascuno da un timestamp che indica il momento in cui sono stati creati (\(\operatorname{t}(posto)\)). A differenza delle normali reti di Petri i gettoni sono quindi distinguibili: questo non significa che due gettoni non possano avere lo stesso timestamp, ma solo che non tutti i gettoni sono uguali (mentre gettoni generati dalla stessa transizione o da transizioni diverse scattate in parallelo avranno invece lo stesso timestamp).

Per ogni transizione viene poi introdotto il concetto di tempo di abilitazione (\(\bf{enab}\)), ovvero il momento in cui la transizione viene abilitata: poiché una transizione è abilitata quando tutti i posti nel suo preset contengono tanti gettoni quanto il peso dell’arco entrante in essa, il tempo di abilitazione di una transizione sarà pari al massimo tra i timestamp dei gettoni che compongono la tupla abilitante.
Poiché i posti nel preset della transizione potrebbero contenere più gettoni di quelli necessari per farla scattare, una transizione potrebbe avere più tempi di abilitazione diversi in base ai gettoni considerati per la tupla abilitante.

Ovviamente i tempi di scatto delle transizioni non potranno essere minori del tempo di abilitazione, in quanto una transizione non può scattare prima di essere abilitata. Gli insiemi dei tempi di scatto potranno invece dipendere dal tempo di abilitazione: così, per esempio, una transizione potrebbe scattare 2 secondi dopo essere stata abilitata, oppure tra 3 e 5 minuti dall’abilitazione.
A tal proposito, molto spesso i tempi di scatto saranno rappresentati come intervalli \([min,max]\) piuttosto che come insiemi: nei nostri esempi adotteremo questa convenzione, ma è bene tenere in mente che tali insiemi potrebbero avere qualunque possibile forma.

Definizioni matematiche

Facciamo un po’ di chiarezza introducendo delle definizioni rigorose per tutto quanto citato nell’introduzione.
Una rete Time Basic è una 6-tupla del tipo \(\langle P, T, \Theta, F, tf, m_0 \rangle\), dove:

• \(P, T, F\) sono identici all’insieme dei posti, delle transizioni e al flusso delle normali reti di Petri;

• \(\Theta\) (theta) è il dominio temporale, ovvero l’insieme numerico che contiene le rappresentazioni degli istanti di tempo;

• \(tf\) è una funzione che associa ad ogni transizione \(t \in T\) una funzione temporale \(\operatorname{tf_{t}}\) che data in input la tupla abilitante \(\bf{en}\), ovvero l’insieme dei timestamp dei gettoni scelti per l’abilitazione nel preset, restituisce un insieme di tempi di scatto possibili:

  $$ \operatorname{tf_{t}}(en) \subseteq \Theta $$

  Per esempio, se per una transizione \(t\) i tempi di scatto sono nell’intervallo \([min, max]\), allora \(\operatorname{tf_{t}}(en) = {r \, \vert \, min \leq r \leq max}\).

• \(m_0\) è un multiset che esprime la marcatura iniziale: si tratta cioè di una funzione che ad ogni posto associa un insieme di coppie timestamp-molteplicità che indicano il numero di gettoni con tale timestamp all’interno del posto:

  $$ m_0 : P \rightarrow { (\theta, \operatorname{mul}(\theta)) \, \vert \, \theta \in \Theta } $$

  Tutte le marcature esprimibili per le reti Time Basic assumeranno la forma di simili funzioni.

Con questi costrutti matematici siamo in grado di descrivere completamente lo stato di una rete Time Basic. Tuttavia sorge ora spontanea una domanda: dovendo modellare il concetto di tempo, come evolve una rete TB?