Criterio di copertura delle condizioni
Un test \(\ T\) soddisfa il criterio di copertura delle condizioni se e solo se ogni singola condizione (effettiva) viene resa sia vera che falsa in corrispondenza di almeno un caso di test \(\ t \in T\).
Similmente ai criteri precedenti, la metrica è quindi la percentuale delle condizioni che sono state rese sia vere che false su quelle per cui è possibile farlo.
Sebbene simile, si tratta di un criterio diverso da quello di copertura delle decisioni: in caso di condizioni composte, come per esempio x != 0 && y < 3, la copertura delle decisioni imporrebbe che l’intera condizione sia resa sia vera che falsa, mentre la copertura delle condizioni richiede di rendere vere e false le singole condizioni atomiche x != 0 e y < 3 in almeno un caso di test.
Come vedremo nell’esempio, ciò non impone quindi di seguire tutti i percorsi sul diagramma di flusso e fa sì che questo criterio non implica il soddisfacimento di nessuno dei precedenti.
| Esempio 3: copertura delle condizioni | |
|---|---|
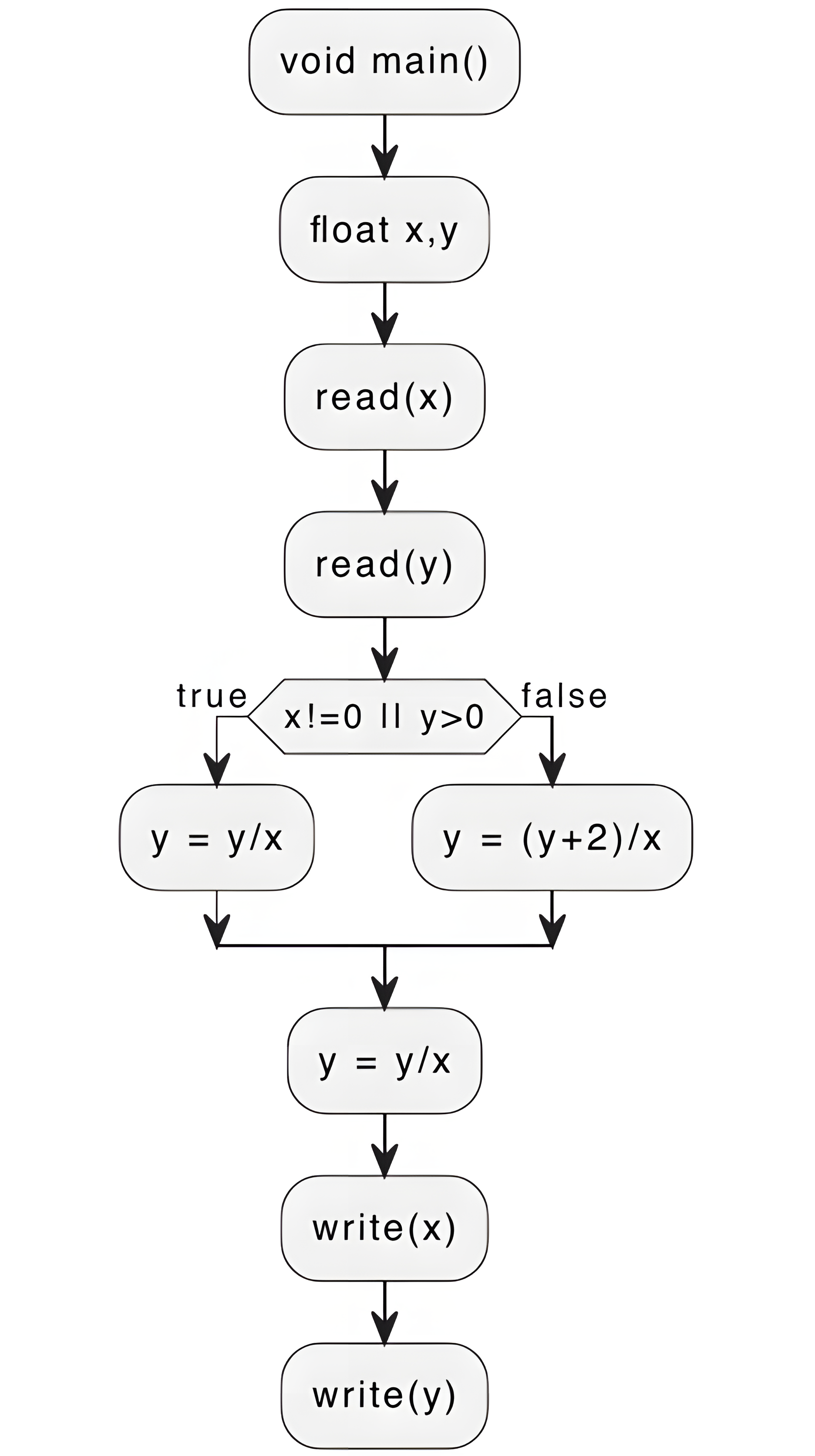
| Pseudocodice | Diagramma di flusso di esecuzione |
|
|
Nell’esempio sopra, il test \( { \langle 0, \, 5 \rangle , \, \langle 5, \, -5 \rangle } \) soddisfa il criterio di copertura della condizioni \
(x != 0 è falsificato da \(\langle 0, \,5 \rangle\) e verificato da \(\langle 5, \, -5 \rangle\), mentre y > 0 è verificato da \(\langle 0, \, 5 \rangle\) e falsificato da \(\langle 5, \, -5 \rangle\)), ma la decisione è sempre vera.
Sono infatti presenti anomalie alla riga 6 (possibile divisione per zero) e alla riga 8 (overflow e divisione per zero), ma i comandi contenuti nella riga 8 non sono coperti. In questo caso più che mai, quindi, la copertura delle condizioni non garantisce la correttezza del programma.