Vitalità di una transizione

Una transizione \(t\) in una marcatura \(M\) si può dire viva con un certo grado:

• grado 0 (o morta): non è abilitata in nessuna marcatura appartanente all’insieme di raggiungibilità, quindi qualunque evoluzione avvenga nella rete, la transizione non portà mai scattare (non è sempre un aspetto negativo);
• grado 1: esiste almeno una marcatura raggiungibile a partire da \(M\) in cui la transizione è abilitata;
• grado 2: per ogni numero \(n\) naturale escluso lo zero esiste almeno una sequenza di scatti ammissibile a partire da \(M\) in cui la transizione scatta \(n\) volte, ovvero è possibile far scattare la transizione un numero \(n\) grande a piacere di volte;
• grado 3: esiste una sequenza di scatti ammissibile a partire da \(M\) per cui la transizione scatta infinite volte;
• grado 4 in qualunque marcatura raggiungibile esiste una sequenza ammissibile in cui è possibile far scattare la transizione almeno una volta, di conseguenza può scattare infinite volte in qualunque situazione ci si trovi (ovvero in qualunque marcatura).
  In questo caso si dice che la transizione è viva in maniera assoluta.

Si noti come il concetto di \(n\) grande a piacere presente nel grado 2 sia differente dal concetto di infinite volte nel grado.

Gli esempi seguenti rappresentano delle situazioni verosimili riguardanti la vitalità delle transizioni:

• grado 0: qualunque cosa accada la centrale nucleare non può esplodere;
• grado 1: in un certo momento se si assume il controllo di tutto ciò che avverrà è possibile portare la centrale nucleare allo spegnimento;
• grado 2: Duccio, ingegnere della centrale nucleare che si trova in coffee break, è in grado di interagire con la macchinetta del caffé appena accesa in modo da avere un numero di caffé grande a piacere, almeno finchè qualcuno non inserisce una moneta nella macchinetta;
• grado 3: Biascica, guardia giurata della centrale, è in grado di fare alzare la sbarra per il parcheggio un numero infinito di volte;
• grado 4: se succede qualcosa fuori dal controllo all’interno della centrale si può comunque riuscire ad eseguire lo spegnimento (René urla “chiudi tutto, Duccio!”).

Una rete viene chiamata viva quando tutte le sue transizioni sono vive.

Esempio

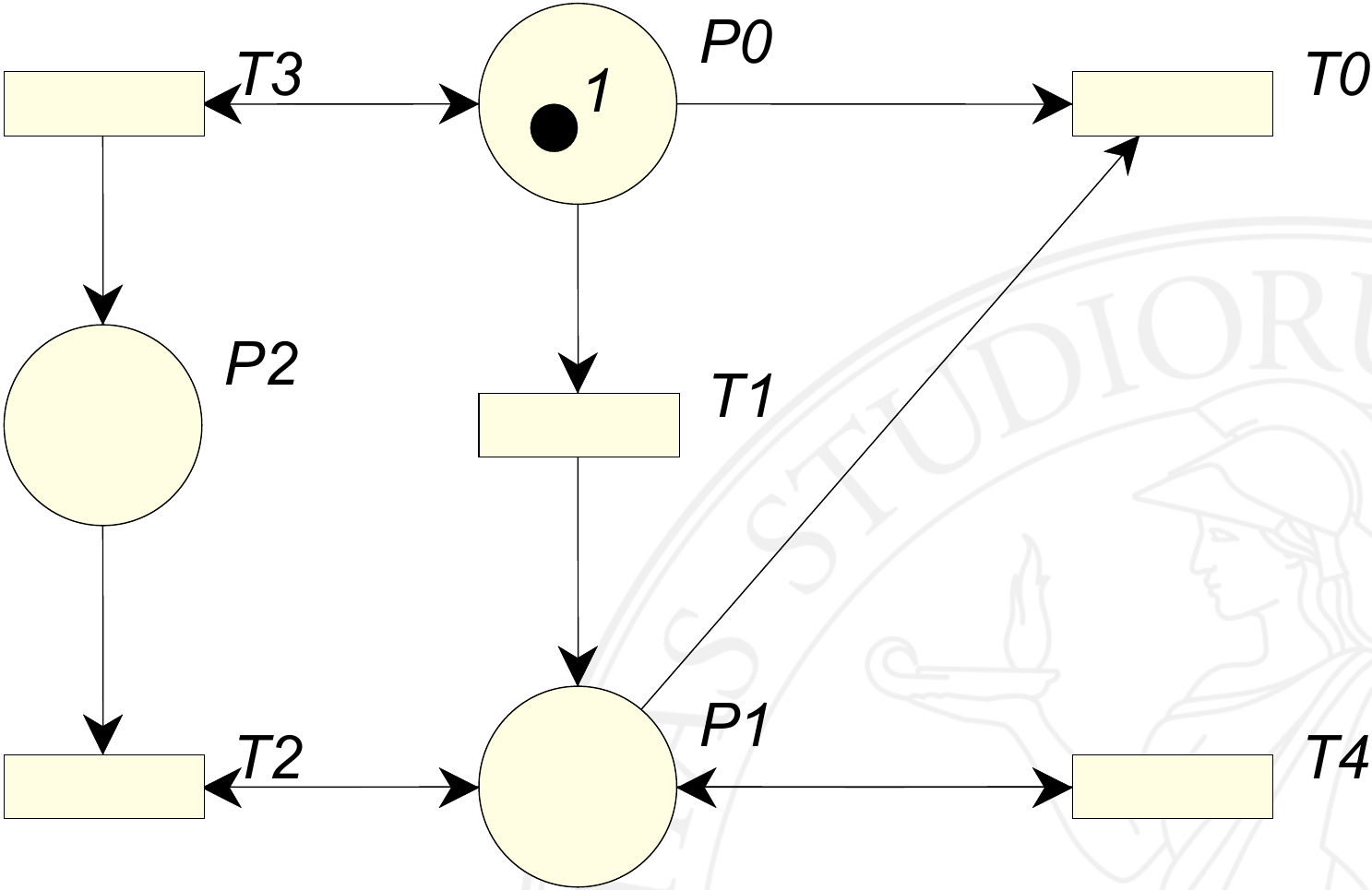
• Da questo esempio pratico è possibile notare come la transizione \(t_0\) è di grado 0 in quanto non potrà mai scattare, perchè è impossibile che abbia i gettoni necessari nel preset per scattare (al massimo o in \(p_0\) o in \(p_1\)).
• La transizione \(t_1\) è di grado 1 perchè esiste almeno una marcatura raggiungibile per cui essa scatti, infatti la marcatura corrente è quella che ne permette lo scatto (ricordando ancora che se una transizione è abilitata allo scatto non significa che debba scattare).
• Osservando la transizione \(t_3\) è possibile notare che essa scatti infinite volte (e non \(n\) grande a piacere, quindi non si tratta di una transizione di grado 2), ma nel caso avvenga lo scatto di \(t_1\) la transizione \(t_3\) non potrà mai più essere abilitata (quindi esiste una marcatura in cui non sarà possibile il suo scatto) garantendo che non si tratta di una transizione di grado 4, ma bensì di grado 3.
• Il caso più particolare è quello della transizione \(t_2\): è noto che \(t_3\) può scattare infinite volte e quindi in \(p_2\) possono esserci infiniti gettoni; inoltre, conseguentemente allo scatto di \(t_1\) il posto \(p_1\) conterrà un gettone, ma comunque la transizione \(t_2\) non può scattare infinite volte. Questo perchè è vero che all’infinito posso generare gettoni in \(p_2\), ma dal momento che scatta \(t_1\) si perde questa possibilità, permettendo a \(t_2\) di scattare tante volte quanti sono i gettoni in \(p_2\). La transazione è quindi di grado 2.
• Infine \(t_4\) è una transizione viva (di grado 4), perchè qualunque sia la marcatura raggiungibile dalla marcatura corrente è possibile prendere il controllo e sicuramente esiste una sequenza di scatti tale per cui \(t_4\) diventi abilitata.